题目内容
11．已知a＞0，b＞0，a+b=1，则$\frac{1}{a}$+$\frac{4}{b}$的最小值是（ ）| A． | 4 | B． | 5 | C． | 8 | D． | 9 |
分析 结合乘“1”法，通过基本不等式求解最值即可．
解答 解：∵a＞0，b＞0，a+b=1，
∴$\frac{1}{a}$+$\frac{4}{b}$=（$\frac{1}{a}$+$\frac{4}{b}$）（a+b）=5+$\frac{b}{a}$+$\frac{4a}{b}$≥5+2 $\sqrt{\frac{b}{a}•\frac{4a}{b}}$=9，
当且仅当b=2a=$\frac{2}{3}$时取等号．
故选：9．
点评 本题考查了乘“1”法在基本不等式的应用，考查基本不等式的性质以及计算能力．
练习册系列答案
相关题目
10．在某地区2008年至2014年中，每年的居民人均纯收入y（单位：千元）的数据如表：
对变量t与y进行相关性检验，得知t与y之间具有线性相关关系．
（1）求y关于t的线性回归方程；
（2）预测该地区2017年的居民人均纯收入．
附：回归直线的斜率和截距的最小二乘估计公式分别为：$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}（{t}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{t}_{i}-\overline{t}）^{2}}$，$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{t}$．
| 年 份 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 |
| 年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 人均纯收入y | 2.7 | 3.6 | 3.3 | 4.6 | 5.4 | 5.7 | 6.2 |
（1）求y关于t的线性回归方程；
（2）预测该地区2017年的居民人均纯收入．
附：回归直线的斜率和截距的最小二乘估计公式分别为：$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}（{t}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{t}_{i}-\overline{t}）^{2}}$，$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{t}$．
2．若a-b＞0，下列不等式一定成立的个数是（ ）
（1）$\frac{1}{a}＜\frac{1}{b}$（2）$\frac{b}{a}＜1$（3）2a-b＞1（4）ln（a-b）＞0．
（1）$\frac{1}{a}＜\frac{1}{b}$（2）$\frac{b}{a}＜1$（3）2a-b＞1（4）ln（a-b）＞0．
| A． | 3 | B． | 2 | C． | 1 | D． | 0 |
19．已知回归方程为：$\widehat{y}$=3-2x，若解释变量增加1个单位，则预报变量平均（ ）
| A． | 增加2个单位 | B． | 减少2个单位 | C． | 增加3个单位 | D． | 减少3个单位 |
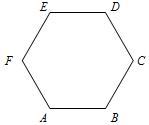如图，点P是边长为1的正六边形ABCDEF的边上的一个动点，设$\overrightarrow{AP}$=x$\overrightarrow{AB}$+y$\overrightarrow{AE}$，则x+y的最大值为2．
16．已知x，y均为正数，且x+y=2，则x+4$\sqrt{xy}$+4y的最大值是（ ）
| A． | 8 | B． | 9 | C． | 10 | D． | 11 |