题目内容
已知函数f（x）=| cos4x-1 | ||
2cos(
|
（1）求函数f（x）的最小正周期和单调递减区间；
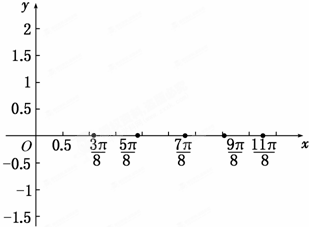
（2）在所给坐标系中画出函数在区间[
| 3 |
| 8 |
| 11 |
| 8 |
考点：由y=Asin（ωx+φ）的部分图象确定其解析式,三角函数中的恒等变换应用,三角函数的周期性及其求法
专题：三角函数的图像与性质,解三角形
分析：（1）利用二倍角公式和两角和公式对函数解析式进行化简，利用三角函数的性质求得函数最小正周期和单调减区间．
（2）根据函数解析式知，
，听过五个点画出图象．
（2）根据函数解析式知，
，听过五个点画出图象．解答：
解：f（x）=
+cos 2x=sin 2x+cos 2x=
sin（2x+
）．
（1）∴函数f（x）的最小正周期T=
=π，
当2kπ+
≤2x+
≤2kπ+
π，k∈Z，时，即2kπ+
≤2x≤2kπ+
π，k∈Z，故kπ+
≤x≤kπ+
π，k∈Z．
∴函数f（x）的单调递减区间为[kπ+
，kπ+
π]（k∈Z）．
（2）图象如下：
| 1-2sin22x-1 |
| -2sin2x |
| 2 |
| π |
| 4 |
（1）∴函数f（x）的最小正周期T=
| 2π |
| 2 |
当2kπ+
| π |
| 2 |
| π |
| 4 |
| 3 |
| 2 |
| π |
| 4 |
| 5 |
| 4 |
| π |
| 8 |
| 5 |
| 8 |
∴函数f（x）的单调递减区间为[kπ+
| π |
| 8 |
| 5 |
| 8 |
（2）图象如下：
点评：本题主要考查了三角函解析式问题．在解决三角形问题时注意参照图象．
练习册系列答案
相关题目
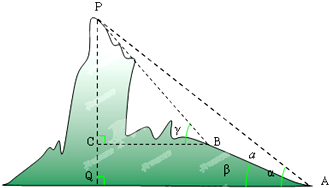如图，在山脚A测得出山顶P的仰角为α，沿倾斜角为β的斜坡向上走a米到B，在B处测得山顶P的仰角为γ，求证：山高h=
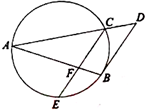如图，已知AB和AC是圆的两条弦，过点B作圆的切线与AC的延长线相交于D，过点C作BD的平行线与圆交于点E，与AB相交于点F，AF=6，FB=2，EF=3，则线段CD的长为