题目内容
已知函数y=sin2x+
sinxcosx+2cos2x,求:
(1)函数的最小值及此时的x的集合.
(2)函数在[0,π]上的单调区间.
| 3 |
(1)函数的最小值及此时的x的集合.
(2)函数在[0,π]上的单调区间.
考点:三角函数中的恒等变换应用,正弦函数的图象
专题:三角函数的图像与性质
分析:(1)根据二倍角公式,化简函数解析式:f(x)=sin(2x+
)+
,然后,结合三角寒山寺的图象与性质求解最值问题;
(2)直接结合三角函数的单调性进行求解即可.
| π |
| 6 |
| 3 |
| 2 |
(2)直接结合三角函数的单调性进行求解即可.
解答:
解:(1)∵y=sin2x+
sinxcosx+2cos2x,
=cos2x+
sinxcosx+cos2x+sin2x
=cos2x+
sinxcosx+1
=
+
sin2x+1
=
sin2x+
cos2x+
=sin(2x+
)+
∴f(x)=sin(2x+
)+
∴ymin=1+
=
,此时,2x+
=-
+2kπ,k∈Z,
∴x=-
+kπ,k∈Z,
∴函数的最小值
,及此时的x的集合{x|x=-
+kπ,k∈Z}.
(2)令-
+2kπ≤2x+
≤
+2kπ,k∈Z,
∴-
+kπ≤x≤
+kπ,
∴函数在[0,π]上的单调增区间[0,
],[
,π],
令
+2kπ≤2x+
≤
+2kπ,k∈Z,
∴
+kπ≤x≤
+kπ,
∴函数在[0,π]上的单调减区间[
,
]
综上,函数在[0,π]上的单调增区间为:[0,
],[
,π],
减区间为:[
,
].
| 3 |
=cos2x+
| 3 |
=cos2x+
| 3 |
=
| 1+cos2x |
| 2 |
| ||
| 2 |
=
| ||
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
=sin(2x+
| π |
| 6 |
| 3 |
| 2 |
∴f(x)=sin(2x+
| π |
| 6 |
| 3 |
| 2 |
∴ymin=1+
| 3 |
| 2 |
| 5 |
| 2 |
| π |
| 6 |
| π |
| 2 |
∴x=-
| π |
| 3 |
∴函数的最小值
| 5 |
| 2 |
| π |
| 3 |
(2)令-
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
∴-
| π |
| 3 |
| π |
| 6 |
∴函数在[0,π]上的单调增区间[0,
| π |
| 6 |
| 2π |
| 3 |
令
| π |
| 2 |
| π |
| 6 |
| 3π |
| 2 |
∴
| π |
| 6 |
| 2π |
| 3 |
∴函数在[0,π]上的单调减区间[
| π |
| 6 |
| 2π |
| 3 |
综上,函数在[0,π]上的单调增区间为:[0,
| π |
| 6 |
| 2π |
| 3 |
减区间为:[
| π |
| 6 |
| 2π |
| 3 |
点评:本题综合考查了三角函数的图象与性质、二倍角公式、三角恒等变换等知识,属于中档题.

练习册系列答案
相关题目
设a=
(3x2-2x)dx,则(ax2-
)6的展开式中的第4项为( )
| ∫ | 2 1 |
| 1 |
| x |
| A、-1280x3 |
| B、-1280 |
| C、240 |
| D、-240 |
执行如图所示的程序框图,若输入n=2014,则输出的S=( )


A、
| ||
B、
| ||
C、
| ||
D、
|
 已知函数f(x)=Asin(φx+φ)的图象,如图求:
已知函数f(x)=Asin(φx+φ)的图象,如图求:

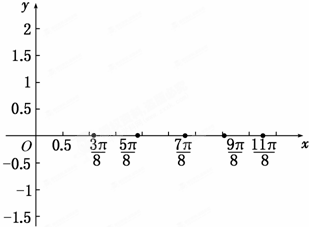 已知函数f(x)=
已知函数f(x)=