题目内容
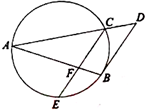如图，已知AB和AC是圆的两条弦，过点B作圆的切线与AC的延长线相交于D，过点C作BD的平行线与圆交于点E，与AB相交于点F，AF=6，FB=2，EF=3，则线段CD的长为考点：与圆有关的比例线段
专题：综合题,立体几何
分析：由相交弦定理可得FC，利用BD∥CF，求出BD=
，AC=
AD，由切割线定理可得结论．
| 16 |
| 3 |
| 3 |
| 4 |
解答：
解：由相交弦定理可得：AF×FB=EF×CF，
∵AF=6，FB=2，EF=3，
∴6×2=3×CF，
∴FC=4，
∵BD∥CF，
∴
=
=
，
∴BD=
，AC=
AD，
由切割线定理可得BD2=DC•DA，
∴
=DC•4DC，
∴DC=
．
故答案为：
．
∵AF=6，FB=2，EF=3，
∴6×2=3×CF，
∴FC=4，
∵BD∥CF，
∴
| CF |
| BD |
| AF |
| AB |
| AC |
| AD |
∴BD=
| 16 |
| 3 |
| 3 |
| 4 |
由切割线定理可得BD2=DC•DA，
∴
| 256 |
| 9 |
∴DC=
| 8 |
| 3 |
故答案为：
| 8 |
| 3 |
点评：本题考查与圆有关的比例线段，考查相交弦定理、切割线定理，属于中档题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
已知函数f（x）=Asin（φx+φ）的图象，如图求：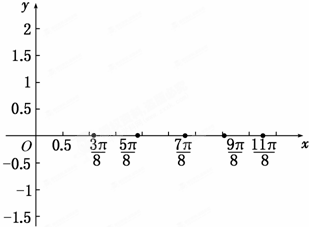
已知函数f（x）=