题目内容
12.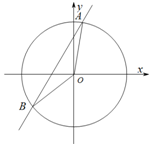 如图,在平面直角坐标系xoy中,直线y=2x+1与圆x2+y2=4相交于A,B两点,则cos∠AOB=( )
如图,在平面直角坐标系xoy中,直线y=2x+1与圆x2+y2=4相交于A,B两点,则cos∠AOB=( )| A. | $\frac{{\sqrt{5}}}{10}$ | B. | $-\frac{{\sqrt{5}}}{10}$ | C. | $\frac{9}{10}$ | D. | $-\frac{9}{10}$ |
分析 求出圆心到直线y=2x+1的距离,由垂径定理得AB,利用余弦定理,可得结论.
解答 解:因为圆心到直线y=2x+1的距离$d=\frac{1}{{\sqrt{4+1}}}=\frac{{\sqrt{5}}}{5}$,
由垂径定理得:${(\frac{1}{2}AB)^2}+{d^2}={R^2}$$⇒A{B^2}=4({r^2}-{d^2})=4×(4-\frac{1}{5})=\frac{76}{5}$
∴由余弦定理有$cos∠AOB=\frac{{4+4-\frac{76}{5}}}{2×2×2}=-\frac{9}{10}$,
故选D.
点评 本题考查点到直线距离公式的运用,考查垂径定理、余弦定理的运用,属于中档题.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
4.定义在R上的奇函数f(x)满足f(x+2)=f(2-x),当x∈[0,2]时,f(x)=-4x2+8x.若在区间[a,b]上,存在m(m≥3)个不同整数xi(i=1,2,…,m),满足$\sum_{i=1}^{m-1}$|f(xi)-f(xi+1)|≥72,则b-a的最小值为( )
| A. | 15 | B. | 16 | C. | 17 | D. | 18 |
19.在△ABC中,D为三角形所在平面内一点,且$\overrightarrow{AD}=\frac{1}{3}\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AC}$,则$\frac{{{S_{△ABD}}}}{{{S_{△ABC}}}}$=( )
| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{2}$ |