题目内容
4.定义在R上的奇函数f(x)满足f(x+2)=f(2-x),当x∈[0,2]时,f(x)=-4x2+8x.若在区间[a,b]上,存在m(m≥3)个不同整数xi(i=1,2,…,m),满足$\sum_{i=1}^{m-1}$|f(xi)-f(xi+1)|≥72,则b-a的最小值为( )| A. | 15 | B. | 16 | C. | 17 | D. | 18 |
分析 根据已知可得函数周期为8,且函数的图形关于x=2对称,从而画出函数图象,结合图象,要使b-a取最小值,则不同整数xi为极值点即可.
解答 解:定义在R上的奇函数f(x)满足f(x+2)=f(2-x),得f(x+2+2)=f(2-x-2)=f(-x)=-f(x),即f(x+4)=-f(x),
则f(x+4)=-f(x+4)=-[-f(x)]=f(x).∴f(x)的周期为8.函数f(x)的图形如下:
比如,当不同整数xi分别为-1,1,2,5,7…时,b-a取最小值,∵f(-1)=-4,f(1)=4,f(2)=0,
至少需要2个+$\frac{1}{4}$个周期,则b-a的最小值为18,
故选:D
点评 本题考查了奇函数的性质,数形结合是解题的关键,属于中档题.

练习册系列答案
相关题目
15.直线l:kx+y+4=0(k∈R)是圆C:x2+y2+4x-4y+6=0的一条对称轴,过点A(0,k)作斜率为1的直线m,则直线m被圆C所截得的弦长为( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\sqrt{2}$ | C. | $\sqrt{6}$ | D. | 2$\sqrt{6}$ |
12.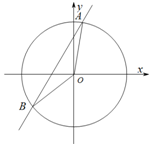 如图,在平面直角坐标系xoy中,直线y=2x+1与圆x2+y2=4相交于A,B两点,则cos∠AOB=( )
如图,在平面直角坐标系xoy中,直线y=2x+1与圆x2+y2=4相交于A,B两点,则cos∠AOB=( )
 如图,在平面直角坐标系xoy中,直线y=2x+1与圆x2+y2=4相交于A,B两点,则cos∠AOB=( )
如图,在平面直角坐标系xoy中,直线y=2x+1与圆x2+y2=4相交于A,B两点,则cos∠AOB=( )| A. | $\frac{{\sqrt{5}}}{10}$ | B. | $-\frac{{\sqrt{5}}}{10}$ | C. | $\frac{9}{10}$ | D. | $-\frac{9}{10}$ |
16.已知抛物线y2=4x与双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)有相同的焦点F,点A是两曲线的一个交点,且AF⊥x轴,则双曲线的离心率为( )
| A. | 2$\sqrt{2}$-1 | B. | $\sqrt{2}$+1 | C. | 8$\sqrt{2}$-8 | D. | 2$\sqrt{2}$-2 |
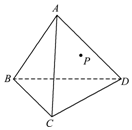 如图,有一个正三棱锥的零件,P是侧面ACD上的一点.过点P作一个与棱AB垂直的截面,怎样画法?并说明理由.
如图,有一个正三棱锥的零件,P是侧面ACD上的一点.过点P作一个与棱AB垂直的截面,怎样画法?并说明理由. 秦九昭是我国南宋时期的数学家,他在所著的《数学九章》中提出的多项式求值的秦九昭算法,至今仍是比较先进的算法,如图所示的程序框图给出了利用秦九昭算法求某多项式值的一个实例,若输入n,x的值分别为3,4,则输出y的值为( )
秦九昭是我国南宋时期的数学家,他在所著的《数学九章》中提出的多项式求值的秦九昭算法,至今仍是比较先进的算法,如图所示的程序框图给出了利用秦九昭算法求某多项式值的一个实例,若输入n,x的值分别为3,4,则输出y的值为( )