题目内容
17.已知函数f(x)=ax3-bx+4,当x=2时,函数f(x)取得极值$-\frac{4}{3}$.(Ⅰ)求函数f(x)的解析式;
(Ⅱ)若方程f(x)=k有3个不等的实数解,求实数k的取值范围.
分析 (Ⅰ)求出函数的导数,利用导函数为0,求出极值点,结合极值,列出方程求解函数f(x)的解析式;
(Ⅱ)利用函数的单调性以及极值,通过f(x)=k有3个不等的实数解,求出k的范围.
解答 解:(Ⅰ)因为f'(x)=3ax2-b,
所以$\left\{\begin{array}{l}f'(2)=12a-b=0\\ f(2)=8a-2b+4=-\frac{4}{3}\;\end{array}\right.$,解得$a=\frac{1}{3}\;,\;b=4$.…(4分)
所以函数的解析式为$f(x)=\frac{1}{3}{x^3}-4x+4$.…(6分)
(Ⅱ)由(Ⅰ)知$f(x)=\frac{1}{3}{x^3}-4x+4$,
所以f'(x)=x2-4=(x+2)(x-2),
所以函数f(x)在(-∞,-2)上递增,在(-2,2)上递减,在(2,+∞)上递增,…(8分)
所以f(x)在x=-2时取得极大值$\frac{28}{3}$,在x=2时取得极小值$-\frac{4}{3}$,…(10分)
因为方程f(x)=k有3个不等的实数解,所以$-\frac{4}{3}<k<\frac{28}{3}$.…(12分)
点评 本题考查函数的极值以及函数的单调性的应用,考查转化思想以及计算能力.

练习册系列答案
相关题目
8.等差数列{an}的前n项和为Sn,且满足a4+a10=20,则S13=( )
| A. | 6 | B. | 130 | C. | 200 | D. | 260 |
12.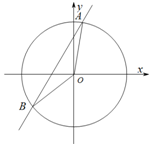 如图,在平面直角坐标系xoy中,直线y=2x+1与圆x2+y2=4相交于A,B两点,则cos∠AOB=( )
如图,在平面直角坐标系xoy中,直线y=2x+1与圆x2+y2=4相交于A,B两点,则cos∠AOB=( )
 如图,在平面直角坐标系xoy中,直线y=2x+1与圆x2+y2=4相交于A,B两点,则cos∠AOB=( )
如图,在平面直角坐标系xoy中,直线y=2x+1与圆x2+y2=4相交于A,B两点,则cos∠AOB=( )| A. | $\frac{{\sqrt{5}}}{10}$ | B. | $-\frac{{\sqrt{5}}}{10}$ | C. | $\frac{9}{10}$ | D. | $-\frac{9}{10}$ |
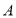 、
、 分别是椭圆
分别是椭圆 :
: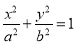 (
( )的上顶点和左焦点,若
)的上顶点和左焦点,若 于圆
于圆 :
: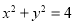 相切于点
相切于点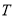 ,且点
,且点 是线段
是线段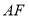 靠近点
靠近点 的三等分点,则椭圆
的三等分点,则椭圆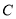 的标准方程为 .
的标准方程为 .