��Ŀ����
7����֪��λ����$\overrightarrow{e_1}��\overrightarrow{e_2}$�ļн�Ϊ$\frac{��}{3}$��$\overrightarrow a=2\overrightarrow{e{\;}_1}-\overrightarrow{e_2}$����$\overrightarrow a$��$\overrightarrow{e_1}$�ϵ�ͶӰ��$\frac{3}{2}$������ ����ƽ������ͶӰ�Ķ��壬���������������������Ӧ��ֵ���ɣ�
��� �⣺��λ����$\overrightarrow{e_1}��\overrightarrow{e_2}$�ļн�Ϊ$\frac{��}{3}$��$\overrightarrow a=2\overrightarrow{e{\;}_1}-\overrightarrow{e_2}$��
��$\overrightarrow a$��$\overrightarrow{e_1}$�ϵ�ͶӰ�ǣ�
|$\overrightarrow{a}$|cos��$\overrightarrow{a}$��$\overrightarrow{{e}_{1}}$��=$\frac{\overrightarrow{a}•\overrightarrow{{e}_{1}}}{|\overrightarrow{{e}_{1}}|}$=$\overrightarrow{a}$•$\overrightarrow{{e}_{1}}$=��2$\overrightarrow{{e}_{1}}$-$\overrightarrow{{e}_{2}}$��•$\overrightarrow{{e}_{1}}$
=2${\overrightarrow{{e}_{1}}}^{2}$-$\overrightarrow{{e}_{1}}$•$\overrightarrow{{e}_{2}}$
=2-1��1��1��cos$\frac{��}{3}$
=$\frac{3}{2}$��
�ʴ�Ϊ��$\frac{3}{2}$��
���� ���⿼����ƽ��������������ͶӰ�ļ������⣬�ǻ�����Ŀ��

| A�� | $\sqrt{2}$ | B�� | 2 | C�� | $2\sqrt{2}$ | D�� | 4 |
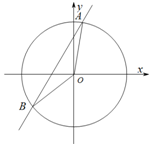 ��ͼ����ƽ��ֱ������ϵxoy�У�ֱ��y=2x+1��Բx2+y2=4�ཻ��A��B���㣬��cos��AOB=��������
��ͼ����ƽ��ֱ������ϵxoy�У�ֱ��y=2x+1��Բx2+y2=4�ཻ��A��B���㣬��cos��AOB=��������| A�� | $\frac{{\sqrt{5}}}{10}$ | B�� | $-\frac{{\sqrt{5}}}{10}$ | C�� | $\frac{9}{10}$ | D�� | $-\frac{9}{10}$ |
| A�� | 2$\sqrt{2}$-1 | B�� | $\sqrt{2}$+1 | C�� | 8$\sqrt{2}$-8 | D�� | 2$\sqrt{2}$-2 |
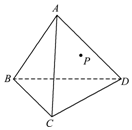 ��ͼ����һ���������������P�Dz���ACD�ϵ�һ�㣮����P��һ������AB��ֱ�Ľ��棬������������˵�����ɣ�
��ͼ����һ���������������P�Dz���ACD�ϵ�һ�㣮����P��һ������AB��ֱ�Ľ��棬������������˵�����ɣ�