题目内容
19.在△ABC中,D为三角形所在平面内一点,且$\overrightarrow{AD}=\frac{1}{3}\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AC}$,则$\frac{{{S_{△ABD}}}}{{{S_{△ABC}}}}$=( )| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{2}$ |
分析 画出图形,利用三角形以及向量关系,求解三角形的面积即可.
解答 解:由已知在△ABC中,D为三角形所在平面内一点,且$\overrightarrow{AD}=\frac{1}{3}\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AC}$,
点D在与AB边平行的中位线上,且为靠近BC边的三等分点处,从而有${S_{△ABD}}=\frac{1}{2}{S_{△ABC}}$.
则$\frac{{{S_{△ABD}}}}{{{S_{△ABC}}}}$=$\frac{1}{2}$.
故选:D.
点评 本题主要考查利用平面向量确定点的位置进而解决平几问题.

练习册系列答案
相关题目
12.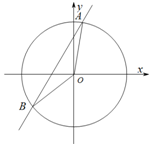 如图,在平面直角坐标系xoy中,直线y=2x+1与圆x2+y2=4相交于A,B两点,则cos∠AOB=( )
如图,在平面直角坐标系xoy中,直线y=2x+1与圆x2+y2=4相交于A,B两点,则cos∠AOB=( )
 如图,在平面直角坐标系xoy中,直线y=2x+1与圆x2+y2=4相交于A,B两点,则cos∠AOB=( )
如图,在平面直角坐标系xoy中,直线y=2x+1与圆x2+y2=4相交于A,B两点,则cos∠AOB=( )| A. | $\frac{{\sqrt{5}}}{10}$ | B. | $-\frac{{\sqrt{5}}}{10}$ | C. | $\frac{9}{10}$ | D. | $-\frac{9}{10}$ |
7.运行如图所示的程序框图,则输出结果为( )


| A. | 1008 | B. | 1009 | C. | 2016 | D. | 2017 |
10. 秦九昭是我国南宋时期的数学家,他在所著的《数学九章》中提出的多项式求值的秦九昭算法,至今仍是比较先进的算法,如图所示的程序框图给出了利用秦九昭算法求某多项式值的一个实例,若输入n,x的值分别为3,4,则输出y的值为( )
秦九昭是我国南宋时期的数学家,他在所著的《数学九章》中提出的多项式求值的秦九昭算法,至今仍是比较先进的算法,如图所示的程序框图给出了利用秦九昭算法求某多项式值的一个实例,若输入n,x的值分别为3,4,则输出y的值为( )
 秦九昭是我国南宋时期的数学家,他在所著的《数学九章》中提出的多项式求值的秦九昭算法,至今仍是比较先进的算法,如图所示的程序框图给出了利用秦九昭算法求某多项式值的一个实例,若输入n,x的值分别为3,4,则输出y的值为( )
秦九昭是我国南宋时期的数学家,他在所著的《数学九章》中提出的多项式求值的秦九昭算法,至今仍是比较先进的算法,如图所示的程序框图给出了利用秦九昭算法求某多项式值的一个实例,若输入n,x的值分别为3,4,则输出y的值为( )| A. | 6 | B. | 25 | C. | 100 | D. | 400 |
7.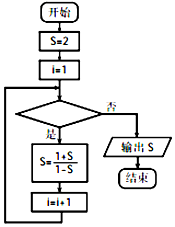 某程序框图如图所示,该程序运行后若输出S的值是2,则判断框内可填写( )
某程序框图如图所示,该程序运行后若输出S的值是2,则判断框内可填写( )
 某程序框图如图所示,该程序运行后若输出S的值是2,则判断框内可填写( )
某程序框图如图所示,该程序运行后若输出S的值是2,则判断框内可填写( )| A. | i≤2015? | B. | i≤2016? | C. | i≤2017? | D. | i≤2018? |
 ,若
,若 ,则实数
,则实数 等于( )
等于( ) B.
B. C.2 D.4
C.2 D.4