题目内容
已知m>0,n>0,向量
=(1,1),
=(m,n-1),且
⊥
,则
+
的最小值是 .
| a |
| b |
| a |
| b |
| 2 |
| m |
| 4 |
| n |
考点:平面向量数量积的运算,基本不等式
专题:平面向量及应用,不等式
分析:根据两向量垂直的充要条件容易得到m+n=1,所以
+
=(m+n)(
+
)=
+
+6,而根据基本不等式
+
≥4
,这样便可求出
+
的最小值.
| 2 |
| m |
| 4 |
| n |
| 2 |
| m |
| 4 |
| n |
| 2n |
| m |
| 4m |
| n |
| 2n |
| m |
| 4m |
| n |
| 2 |
| 2 |
| m |
| 4 |
| n |
解答:
解:∵
⊥
;
∴
•
=m+n-1=0;
∴m+n=1;
又m>0,n>0;
∴
+
=(m+n)(
+
)=
+
+6≥2
+6=4
+6,当
=
,即n=
m时取“=”;
∴
+
的最小值为4
+6.
故答案为:4
+6.
| a |
| b |
∴
| a |
| b |
∴m+n=1;
又m>0,n>0;
∴
| 2 |
| m |
| 4 |
| n |
| 2 |
| m |
| 4 |
| n |
| 4m |
| n |
| 2n |
| m |
| 8 |
| 2 |
| 4m |
| n |
| 2n |
| m |
| 2 |
∴
| 2 |
| m |
| 4 |
| n |
| 2 |
故答案为:4
| 2 |
点评:考查两非零向量垂直的充要条件,掌握根据m+n=1,而对
+
乘以m+n的方法,基本不等式的运用,并注意基本不等式所具备的条件.
| 2 |
| m |
| 4 |
| n |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知函数f(x)=x2+1的图象在点A(x1,f(x1))与点B(x2,f(x2))处的切线互相垂直,并交于点P,则点P的坐标可能是( )
A、(
| ||
B、(0,
| ||
| C、(1,3) | ||
D、(1,
|
一个几何体的三视图如图所示,则该几何体的外接球的表面积为( )
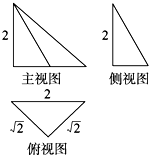

| A、36π | ||
| B、8π | ||
C、
| ||
D、
|
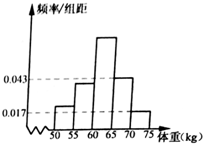 某校为了解2015届高三毕业班准备考飞行员学生的身体素质,对他们的体重进行了测量,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右前3个小组的频率之比为1:2:4,其中第二小组的频率为11.
某校为了解2015届高三毕业班准备考飞行员学生的身体素质,对他们的体重进行了测量,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右前3个小组的频率之比为1:2:4,其中第二小组的频率为11.