题目内容
已知平面上的曲线C及点P,在C上任取一点Q,定义线段PQ长度的最小值为点P到曲线C的距离,记作d(P,C).若曲线C1表示直线x=-
,曲线C2表示射线y=0(x≥
),则点集{P|d(P,C1)=d(P,C2)}所表示的图形是( )
| 1 |
| 2 |
| 1 |
| 2 |
A、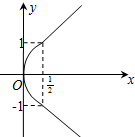 |
B、 |
C、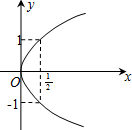 |
D、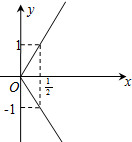 |
考点:曲线与方程
专题:综合题,函数的性质及应用
分析:当-1≤y≤1时,点集为{P|d(P,C1)=|PC|},当y≤-1或y≥1时,点集{P|d(P,C1)=d(P,C2)},确定表示的图形,即可得出结论.
解答:
解:设P(x,y),点A(0,-1),B(0,1),C(
,0),
当-1≤y≤1时,点集为{P|d(P,C1)=|PC|},表示的图形是抛物线y2=2x上的一段,其中 0≤x≤
;
当y≤-1或y≥1时,点集{P|d(P,C1)=d(P,C2)},表示的图形分别是直线x=-
与x轴正方向夹角的平分线上的一条射线,即y=x+
(x≥
)和y=-x-
(x≥
).对比选项知A正确.
故选:A.
| 1 |
| 2 |
当-1≤y≤1时,点集为{P|d(P,C1)=|PC|},表示的图形是抛物线y2=2x上的一段,其中 0≤x≤
| 1 |
| 2 |
当y≤-1或y≥1时,点集{P|d(P,C1)=d(P,C2)},表示的图形分别是直线x=-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故选:A.
点评:本题考查了分段函数的解析式的求法及其图象的作法,对于分段函数一般选用数形结合和分类讨论的数学思想进行解题.根据不同的范围研究不同的解析式,从而选定用分段函数来表示.属于中档题.

练习册系列答案
相关题目
函数f(x)=2cosx(x∈[-π,π])的图象大致为( )
A、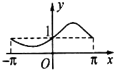 |
B、 |
C、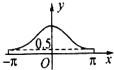 |
D、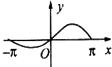 |
已知{an}是等差数列,若2a7-a5-3=0,则a9的值是( )
| A、9 | B、6 | C、3 | D、1 |