题目内容
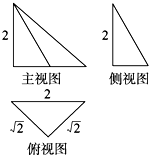
一个几何体的三视图如图所示，则该几何体的外接球的表面积为（ ）
| A、36π | ||
| B、8π | ||
C、
| ||
D、
|
考点：由三视图求面积、体积
专题：空间位置关系与距离
分析：根据几何体的三视图得出该几何体是直三棱锥，且底面是等腰直角三角形，
根据直三棱锥的外接球是对应直三棱柱的外接球，由外接球的结构特征，求出它的半径与表面积．
根据直三棱锥的外接球是对应直三棱柱的外接球，由外接球的结构特征，求出它的半径与表面积．
解答：
解：根据几何体的三视图，得；
该几何体是底面为等腰直角三角形，高为2的直三棱锥；
如图所示；
则该直三棱锥的外接球是对应直三棱柱的外接球，
设几何体外接球的半径为R，
∵底面是等腰直角三角形，∴底面外接圆的半径为1，
∴R2=1+1=2，
∴外接球的表面积是4πR2=8π．
故选：B．
该几何体是底面为等腰直角三角形，高为2的直三棱锥；
如图所示；
则该直三棱锥的外接球是对应直三棱柱的外接球，
设几何体外接球的半径为R，
∵底面是等腰直角三角形，∴底面外接圆的半径为1，
∴R2=1+1=2，
∴外接球的表面积是4πR2=8π．
故选：B．
点评：本题考查了根据几何体的三视图求对应的几何体的表面积的应用问题，是基础题目．
练习册系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
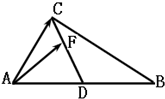如图所示，在△ABC中，D为AB的中点，F在线段CD上，设| AB |
| a |
| AC |
| b |
| AF |
| a |
| b |
| 1 |
| x |
| 2 |
| y |
A、8+2
| ||
| B、8 | ||
| C、6 | ||
D、6+2
|
函数f（x）=2cosx（x∈[-π，π]）的图象大致为（ ）
A、 |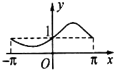
B、 |
C、 |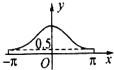
D、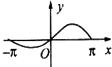 |