题目内容
2.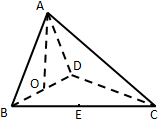 如图,四面体ABCD中,O、E分别为BD、BC的中点,且CA=CB=CD=BD=$\sqrt{2}$,AB=AD=1,则异面直线AB与CD所成角的正切值为.( )
如图,四面体ABCD中,O、E分别为BD、BC的中点,且CA=CB=CD=BD=$\sqrt{2}$,AB=AD=1,则异面直线AB与CD所成角的正切值为.( )| A. | $\sqrt{7}$ | B. | $\frac{\sqrt{7}}{8}$ | C. | $\frac{\sqrt{2}}{4}$ | D. | $\sqrt{2}$ |
分析 取AC的中点M,连结OM、ME、OE,则直线OE与EM所成的锐角∠OEM就是异面直线AB与CD所成的角,由此能求出异面直线AB与CD所成角的正切值.
解答 解:取AC的中点M,连结OM、ME、OE,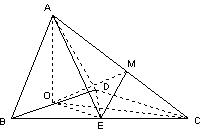
由E为BC的中点知ME∥AB,OE∥DC,
∴直线OE与EM所成的锐角∠OEM就是异面直线AB与CD所成的角,
在△OME中,EM=$\frac{1}{2}AB$=$\frac{1}{2}$,OE=$\frac{1}{2}DC$=$\frac{\sqrt{2}}{2}$,
∵OM是直角△AOC斜边AC上的中线,
∴OM=$\frac{1}{2}AC$=$\frac{\sqrt{2}}{2}$,
∴cos∠OEM=$\frac{E{O}^{2}+E{M}^{2}-O{M}^{2}}{2×EO×EM}$=$\frac{\frac{1}{2}+\frac{1}{4}-\frac{1}{2}}{2×\frac{\sqrt{2}}{2}×\frac{1}{2}}$=$\frac{\sqrt{2}}{4}$.
tan∠OEM=$\sqrt{7}$.
∴异面直线AB与CD所成角的正切值为$\sqrt{7}$.
故选:A.
点评 本题考查异面直线所成角的正切值的求法,是中档题,解题时要认真审题,注意空间能力的培养.

练习册系列答案
相关题目
8.已知A(1,3),B(-5,1),以AB为直径的圆的标准方程是( )
| A. | (x+2)2+(y-2)2=10 | B. | (x+2)2+(y-2)2=40 | C. | (x-2)2+(y+2)2=10 | D. | (x-2)2+(y+2)2=40 |
13.方程ex=2-x的解所在的一个区间为( )
| A. | (-2,-1) | B. | (-1,0) | C. | (0,1) | D. | (1,2) |
14.直线y=5与y=-1在区间$[{0\;,\;\;\frac{4π}{ω}}]$上截曲线$y=msin\frac{ω}{2}x+n({m>0\;,\;\;n>0})$所得弦长相等且不为零,则下列描述正确的是( )
| A. | $m≤\frac{3}{2}\;,\;\;n=\frac{5}{2}$ | B. | m≤3,n=2 | C. | $m>\frac{3}{2}$ | D. | m>3,n=2 |
11.已知a=${4}^{\frac{1}{2}}$,b=${2}^{\frac{1}{3}}$,c=${5}^{\frac{1}{2}}$,则a、b、c的大小关系为( )
| A. | b<a<c | B. | a<b<c | C. | b<c<a | D. | c<a<b |