题目内容
7．求下列各式的值：（1）${2^{4+{{log}_2}3}}$
（2）${0.064^{-\frac{1}{3}}}-{（-\frac{7}{8}）^0}+{[{（-2）^3}]^{-\frac{4}{3}}}+{16^{-0.75}}+{0.01^{\frac{1}{2}}}$．
分析 （1）利用对数的运算性质即可得出．
（2）利用指数的运算性质即可得出．
解答 解：（1）原式=${2}^{4}×{2}^{lo{g}_{2}3}$=16×3=48．
（2）原式=$0．{4}^{3×（-\frac{1}{3}）}$-1+2-4+${2}^{4×（-\frac{3}{4}）}$+0.1
=$\frac{5}{2}$-1+$\frac{1}{16}$+$\frac{1}{8}$+0.1
=$\frac{143}{80}$．
点评 本题考查了指数与对数的运算性质，考查了推理能力与计算能力，属于基础题．
练习册系列答案
世纪百通期末金卷系列答案
相关题目
18．“a＞b”是“a2＞b2”的__________条件（ ）
| A． | 充要条件 | B． | 充分不必要条件 | ||
| C． | 必要不充分条件 | D． | 既不充分也不必要条件 |
2．
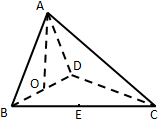如图，四面体ABCD中，O、E分别为BD、BC的中点，且CA=CB=CD=BD=$\sqrt{2}$，AB=AD=1，则异面直线AB与CD所成角的正切值为．（ ）
如图，四面体ABCD中，O、E分别为BD、BC的中点，且CA=CB=CD=BD=$\sqrt{2}$，AB=AD=1，则异面直线AB与CD所成角的正切值为．（ ）| A． | $\sqrt{7}$ | B． | $\frac{\sqrt{7}}{8}$ | C． | $\frac{\sqrt{2}}{4}$ | D． | $\sqrt{2}$ |
一个几何体的三视图如图所示（单位：m），正视图和俯视图的上面均是底边长为12m的等腰直角三角形，下面均是边长为6m的正方形，则该几何体的体积为216+72πm3．