题目内容
12.已知集合 M={(x,y)|y=$\sqrt{25-{x}^{2}}$,y≠0},N={(x,y)|y=-x+b},若M∩N≠∅,则实数b的取值范围是(-5,5$\sqrt{2}$].分析 由M与N,以及两集合交集不为空集,确定出b的范围即可.
解答 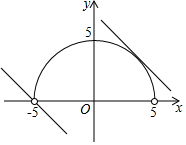 解:画出M与N中两函数图象,如图所示,
解:画出M与N中两函数图象,如图所示,
∵M={(x,y)|y=$\sqrt{25-{x}^{2}}$,y≠0},N={(x,y)|y=-x+b},且M∩N≠∅,
∴半圆y=$\sqrt{25-{x}^{2}}$与y=-x+b有公共点,
当直线y=-x+b与半圆相切时,圆心(0,0)到直线y=-x+b的距离d=r,即$\frac{|b|}{\sqrt{2}}$=5,
解得:b=5$\sqrt{2}$(负值舍去),
把(-5,0)代入y=-x+b得:b=-5,
则实数b的范围是(-5,5$\sqrt{2}$],
故答案为:(-5,5$\sqrt{2}$]
点评 此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.

练习册系列答案
相关题目
2.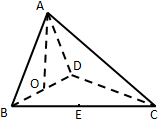 如图,四面体ABCD中,O、E分别为BD、BC的中点,且CA=CB=CD=BD=$\sqrt{2}$,AB=AD=1,则异面直线AB与CD所成角的正切值为.( )
如图,四面体ABCD中,O、E分别为BD、BC的中点,且CA=CB=CD=BD=$\sqrt{2}$,AB=AD=1,则异面直线AB与CD所成角的正切值为.( )
 如图,四面体ABCD中,O、E分别为BD、BC的中点,且CA=CB=CD=BD=$\sqrt{2}$,AB=AD=1,则异面直线AB与CD所成角的正切值为.( )
如图,四面体ABCD中,O、E分别为BD、BC的中点,且CA=CB=CD=BD=$\sqrt{2}$,AB=AD=1,则异面直线AB与CD所成角的正切值为.( )| A. | $\sqrt{7}$ | B. | $\frac{\sqrt{7}}{8}$ | C. | $\frac{\sqrt{2}}{4}$ | D. | $\sqrt{2}$ |
3.在数列{an}中,a1=2,2an+1=2an+1,则a2015的值是( )
| A. | 1009 | B. | 1008 | C. | 1010 | D. | 1011 |
7.已知正四面体棱长为4$\sqrt{2}$,则此正四面体外接球的表面积为( )
| A. | 36π | B. | 48π | C. | 64π | D. | 72π |
4.已知三条直线m,n,l,三个平面α,β,γ,下面说法正确的是( )
| A. | $\left.\begin{array}{l}{α⊥γ}\\{β⊥γ}\end{array}\right\}$⇒α∥β | B. | $\left.\begin{array}{l}{m⊥l}\\{n⊥l}\end{array}\right\}$⇒m∥n | C. | $\left.\begin{array}{l}{m∥β}\\{l⊥m}\end{array}\right\}$⇒l∥β | D. | $\left.\begin{array}{l}{m∥n}\\{n⊥γ}\end{array}\right\}$⇒m⊥γ |
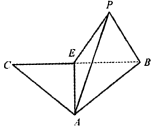 等腰三角形ABC,E为底边BC的中点,沿AE折叠,如图,将C折到点P的位置,使P-AE-C为120°,设点P在面ABE上的射影为H.
等腰三角形ABC,E为底边BC的中点,沿AE折叠,如图,将C折到点P的位置,使P-AE-C为120°,设点P在面ABE上的射影为H.