题目内容
已知直线x+2y-3=0与圆x2+y2+x-6y+m=0相交于P,Q两点,且OP⊥OQ(O为坐标原点),求实数m的值.
考点:直线与圆相交的性质
专题:直线与圆
分析:将直线和圆进行联立,利用根与系数之间的关系建立条件方程,即可求出m的值.
解答:
j解:由题意设P(x1,y1),Q(x2,y2),
则由方程组
,
消y得5x2+10x+4m-27=0,
于是根据韦达定理得,x1+x2=-2,x1x2=
,
y1y2=
(3-x1)?
(3-x2)=
[9-3(x1+x2)+x1x2]=
[9+6+
]=
,
∵OP⊥OQ,
∴kOP?kOQ=
=-1,
故x1x2+y1y2=0,
从而可得
+
=0,
解得m=3.
则由方程组
|
消y得5x2+10x+4m-27=0,
于是根据韦达定理得,x1+x2=-2,x1x2=
| 4m-27 |
| 5 |
y1y2=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 4m-27 |
| 5 |
| m+12 |
| 5 |
∵OP⊥OQ,
∴kOP?kOQ=
| y1y2 |
| x1x2 |
故x1x2+y1y2=0,
从而可得
| m+12 |
| 5 |
| 4m-27 |
| 5 |
解得m=3.
点评:本题主要考查直线和圆的位置关系的应用,联立方程组利用根与系数之间的关系建立条件即可,考查学生的计算能力.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
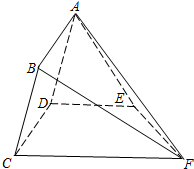 如图,矩形ABCD所在的半平面和直角梯形CDEF所在的半平面成60°的二面角,DE∥CF,CD⊥DE,AD=2,
如图,矩形ABCD所在的半平面和直角梯形CDEF所在的半平面成60°的二面角,DE∥CF,CD⊥DE,AD=2,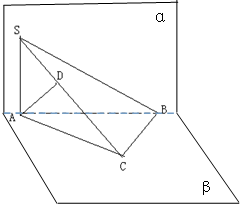 已知直二面角α-AB-β中,S∈平面α,C∈平面β,∠ACB=90°,SA⊥AB,AD⊥SC于D,
已知直二面角α-AB-β中,S∈平面α,C∈平面β,∠ACB=90°,SA⊥AB,AD⊥SC于D,