题目内容

已知
OA
=
a
，
OB
=
b
，且|
a
|=|
b
|=4，∠AOB=60°，
（1）求|
a
+
b
|，|
a
-
b
|；
（2）求
a
+
b
与
a
的夹角及
a
-
b
与
a
的夹角．
考点：平面向量数量积的坐标表示、模、夹角
专题：平面向量及应用
分析：（1）利用数量积运算及其性质即可得出；
（2）利用向量的夹角公式即可得出．
解答： 解：（1）∵|
a
|=|
b
|=4，∠AOB=60°，∴
a
•
b
=|
a
| |
b
|cos∠AOB=4×4×cos60°=8．
∴|
a
+
b
|=
a
2+
b
2+2
a
•
b
=
42+42+2×8
=4
3
．
|
a
-
b
|=
a
2+
b
2-2
a
•
b
=
42+42-2×8
=4．
（2）∵
a
•(
a
+
b
)=
a
2+
a
•
b
=42+8=24，
a
•(
a
-
b
)=
a
2-
a
•
b
=42-8=8．
cos＜
a
，
a
+
b
＞=
a
•(
a
+
b
)
|
a
| |
a
+
b
|
=
24
4×4
3
=
3
2
，
cos＜
a
，
a
-
b
＞=
a
•(
a
-
b
)
|
a
| |
a
-
b
|
=
8
4×4
=
1
2
．
∴＜
a
，
a
+
b
＞=30°，
＜
a
，
a
-
b
＞=60°．
点评：本题考查了数量积运算及其性质、向量的夹角公式，属于基础题．
练习册系列答案
相关题目
已知sin(
π
8
+
α
2
)cos(
π
8
+
α
2
)=
3
4
，α∈(
π
4
，
π
2
)，cos(β-
π
4
)=
3
5
，β∈(
π
2
，π)．
（Ⅰ）求cos(α+
π
4
)的值；
（Ⅱ）求cos（α+β）的值．
已知集合A={x|log2（8-2x）≤2}，B={x|
x-5
x+1
＜0}求：
（1）（∁RA）∪B；
（2）（∁RA）∪（∁RB）．
已知椭圆C：
x2
a2
+y2=1（a＞0）的一个焦点为（
3
，0）．
（1）求a的值．
（2）直线l经过点P（
1
2
，
1
2
），且与椭圆C交于A、B两点，若点P恰为线段AB的中点，求直线l的方程．
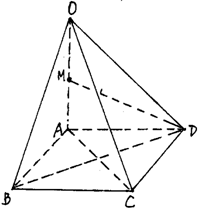如图，在四棱锥O-ABCD中，底面ABCD是边长为1的正方形，OA⊥底面ABCD，OA=2，M为OA中点．
（1）求证：直线BD⊥平面OAC；
（2）求直线MD与平面OAC所成角的大小；
（3）求点A到平面OBD的距离．
在平面直角坐标系xOy中，已知椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）与直线l：x=m（m∈R）．四点（3，1），（3，-1），（-2
2
，0），（
3
，
3
）中有三个点在椭圆C上，剩余一个点在直线l上．
（1）求椭圆C的方程；
（2）若动点P在直线l上，过P作直线交椭圆C于M，N两点，使得PM=PN，再过P作直线l′⊥MN．证明：直线l′恒过定点，并求出该定点的坐标．
已知直线x+2y-3=0与圆x2+y2+x-6y+m=0相交于P，Q两点，且OP⊥OQ（O为坐标原点），求实数m的值．
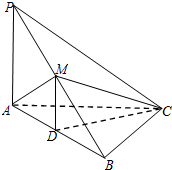如图，在三棱锥P-ABC中，PA⊥AC，PC⊥BC，M为PB的中点，D为AB的中点，且△AMB为正三角形．
（1）求证：BC⊥平面PAC；
（2）若BC=4，PB=10，求点B到平面DCM的距离．
将直线y=-
3
x+2
3
绕点（2，0）按顺时针方向旋转60°所得的直线l在y轴上的截距是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网