题目内容
若 0<α<
,-
<β<0,cos(α+
)=
,cos(
-
)=
,求cos(2α+β)值.
| π |
| 2 |
| π |
| 2 |
| π |
| 4 |
| 1 |
| 3 |
| π |
| 4 |
| β |
| 2 |
| ||
| 3 |
考点:两角和与差的余弦函数
专题:三角函数的求值
分析:由题意求得 sin(α+
)=
,sin(
-
)=
.求得cos(α+
)=cos[(α+
)-(
-
)]的值,从而求得cos(2α+β)=2cos2(α+
)-1的值.
| π |
| 4 |
2
| ||
| 3 |
| π |
| 4 |
| β |
| 2 |
| ||
| 3 |
| β |
| 2 |
| π |
| 4 |
| π |
| 4 |
| β |
| 2 |
| β |
| 2 |
解答:
解:由题意可得
<α+
<
,
<
-
<
,
cos(α+
)=
,cos(
-
)=
,
∴sin(α+
)=
,sin(
-
)=
.
∴cos(α+
)=cos[(α+
)-(
-
)]=cos(α+
)cos(
-
)+sin(α+
)sin(
-
)
=
×
+
×
=
,
∴cos(2α+β)=2cos2(α+
)-1=
.
| π |
| 4 |
| π |
| 4 |
| π |
| 2 |
| π |
| 4 |
| π |
| 4 |
| β |
| 2 |
| π |
| 2 |
cos(α+
| π |
| 4 |
| 1 |
| 3 |
| π |
| 4 |
| β |
| 2 |
| ||
| 3 |
∴sin(α+
| π |
| 4 |
2
| ||
| 3 |
| π |
| 4 |
| β |
| 2 |
| ||
| 3 |
∴cos(α+
| β |
| 2 |
| π |
| 4 |
| π |
| 4 |
| β |
| 2 |
| π |
| 4 |
| π |
| 4 |
| β |
| 2 |
| π |
| 4 |
| π |
| 4 |
| β |
| 2 |
=
| 1 |
| 3 |
| ||
| 3 |
2
| ||
| 3 |
| ||
| 3 |
5
| ||
| 9 |
∴cos(2α+β)=2cos2(α+
| β |
| 2 |
| 23 |
| 27 |
点评:本题主要考查同角三角函数的基本关系,两角和差的三角函数、二倍角公式的应用,属于中档题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
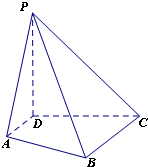 在四棱锥P-ABCD中,PD⊥平面ABCD,PD=CD=BC=2AD,AD∥BC,∠BCD=90°.
在四棱锥P-ABCD中,PD⊥平面ABCD,PD=CD=BC=2AD,AD∥BC,∠BCD=90°.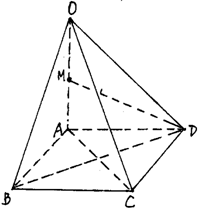 如图,在四棱锥O-ABCD中,底面ABCD是边长为1的正方形,OA⊥底面ABCD,OA=2,M为OA中点.
如图,在四棱锥O-ABCD中,底面ABCD是边长为1的正方形,OA⊥底面ABCD,OA=2,M为OA中点.