题目内容
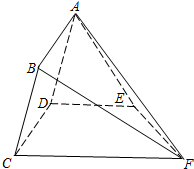 如图,矩形ABCD所在的半平面和直角梯形CDEF所在的半平面成60°的二面角,DE∥CF,CD⊥DE,AD=2,EF=3
如图,矩形ABCD所在的半平面和直角梯形CDEF所在的半平面成60°的二面角,DE∥CF,CD⊥DE,AD=2,EF=3| 2 |
(Ⅰ)求证:BF∥平面ADE;
(Ⅱ)在线段CF上求一点G,使锐二面角B-EG-D的余弦值为
| 1 |
| 4 |
考点:用空间向量求平面间的夹角,直线与平面平行的判定
专题:空间位置关系与距离
分析:(1)利用平面与平面平行的判定定理证明平面BCF∥平面ADE,从而得到BF∥平面ADE.
(2)利用直线与平面,平面与平面垂直的判定定理证明平面CDEF⊥平面ADE,根据平面与平面垂直的性质定理可知,作AO⊥DE于O,则AO⊥平面CDEF.建立如图所示空间直角坐标系,写出点的坐标,利用平面法向量以及锐二面角B-EG-D的余弦值确定G点的坐标,从而确定点G的位置.
(2)利用直线与平面,平面与平面垂直的判定定理证明平面CDEF⊥平面ADE,根据平面与平面垂直的性质定理可知,作AO⊥DE于O,则AO⊥平面CDEF.建立如图所示空间直角坐标系,写出点的坐标,利用平面法向量以及锐二面角B-EG-D的余弦值确定G点的坐标,从而确定点G的位置.
解答:
 证明:(Ⅰ)∵在矩形ABCD中BC∥AD,
证明:(Ⅰ)∵在矩形ABCD中BC∥AD,
AD?平面ADE
BC?平面ADE,
∴BC∥平面ADE,
同理CF∥平面ADE,
又∵BC∩CF=C,
∴平面BCF∥平面ADE,
而BF?平面BCF,
∴BF∥平面ADE.
(Ⅱ)∵CD⊥AD,CD⊥DE
∴∠ADE即为二面角A-CD-F的平面角,
∴∠ADE=60°
又∵AD∩DE=D,
∴CD⊥平面ADE,
又∵CD?平面CDEF
∴平面CDEF⊥平面ADE,
作AO⊥DE于O,则AO⊥平面CDEF.
连结CE,
在△CEF中由余弦定理
cos∠CFE=
,
即
=
∴CE=3
,
易求得,∠ECF=45°,CD=DE=3,OD=1,OE=2.
以O为原点,以平行于DC的直线为x轴,以直线DE为y轴,建立如图空间直角坐标系O-xyz,
则A(0,0,
),B(3,0,
),C(3,-1,0),E(0,2,0),F(3,5,0),
设G(3,t,0),-1≤t≤5,
则
=(-3,2,-
),
=(0,t,-
),
设平面BEG的一个法向量为
=(x,y,z),
则由
,
得
,
取
,
得
=(2-t,3,
t).
平面DEG的一个法向量
=(0,0,1),
∴cos<
,
>=
=
.
为使锐二面角B-EG-D的余弦值为
,
只需
=
,
解得t=
,
此时
=
.
∴G(3,
,0).
即所求的点G为线段CF的靠近C端的四分之一分点.
 证明:(Ⅰ)∵在矩形ABCD中BC∥AD,
证明:(Ⅰ)∵在矩形ABCD中BC∥AD,AD?平面ADE
BC?平面ADE,
∴BC∥平面ADE,
同理CF∥平面ADE,
又∵BC∩CF=C,
∴平面BCF∥平面ADE,
而BF?平面BCF,
∴BF∥平面ADE.
(Ⅱ)∵CD⊥AD,CD⊥DE
∴∠ADE即为二面角A-CD-F的平面角,
∴∠ADE=60°
又∵AD∩DE=D,
∴CD⊥平面ADE,
又∵CD?平面CDEF
∴平面CDEF⊥平面ADE,
作AO⊥DE于O,则AO⊥平面CDEF.
连结CE,
在△CEF中由余弦定理
cos∠CFE=
| |CF|2+|EF|2-|CE|2 |
| 2|CF|•|EF| |
即
| ||
| 2 |
| 36+18-|CE|2 | ||
2•6•3
|
∴CE=3
| 2 |
易求得,∠ECF=45°,CD=DE=3,OD=1,OE=2.
以O为原点,以平行于DC的直线为x轴,以直线DE为y轴,建立如图空间直角坐标系O-xyz,
则A(0,0,
| 3 |
| 3 |
设G(3,t,0),-1≤t≤5,
则
| BE |
| 3 |
| BG |
| 3 |
设平面BEG的一个法向量为
| m |
则由
|
得
|
取
|
得
| m |
| 3 |
平面DEG的一个法向量
| n |
∴cos<
| m |
| n |
(2-t,3,
| ||
|
| ||
|
为使锐二面角B-EG-D的余弦值为
| 1 |
| 4 |
只需
| ||
|
| 1 |
| 4 |
解得t=
| 1 |
| 2 |
此时
| CG |
| CF |
| 1 |
| 4 |
∴G(3,
| 1 |
| 2 |
即所求的点G为线段CF的靠近C端的四分之一分点.
点评:本题考查直线与平面,平面与平面平行及垂直的判定定理,性质定理.平面法向量.以及二面角等知识的综合应用,属于中档题.

练习册系列答案
相关题目
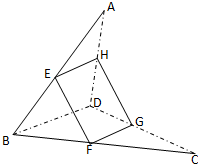 如图,已知四边形ABCD是空间四边形,E是AB的中点,F,G分别是BC,CD上的点,且
如图,已知四边形ABCD是空间四边形,E是AB的中点,F,G分别是BC,CD上的点,且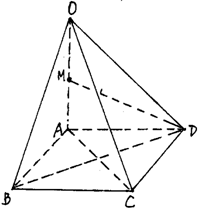 如图,在四棱锥O-ABCD中,底面ABCD是边长为1的正方形,OA⊥底面ABCD,OA=2,M为OA中点.
如图,在四棱锥O-ABCD中,底面ABCD是边长为1的正方形,OA⊥底面ABCD,OA=2,M为OA中点. 如图,在平行六面体ABCD-A1B1C1D1中,E,H分别是AA1、BB1的中点,求证:
如图,在平行六面体ABCD-A1B1C1D1中,E,H分别是AA1、BB1的中点,求证: