题目内容
已知幂函数f(x)=xm2-2m-3(m∈Z)在(0,+∞)是单调减函数,且为偶函数.
(1)求f(x)的解析式;
(2)讨论F(x)=af(x)+(a-2)x5•f(x)的奇偶性,并说明理由.
(1)求f(x)的解析式;
(2)讨论F(x)=af(x)+(a-2)x5•f(x)的奇偶性,并说明理由.
考点:幂函数的性质
专题:函数的性质及应用
分析:(1)根据幂函数的性质,幂函数在(0,+∞)是单调减函数,且为偶函数,得幂指数小于0,再由m∈z可求m的值;
(2)由(I)知F(x)=a•x-4+(a-2)x,分a=0,a=2,a≠0且a≠2三种情况利用定义分别判断函数的奇偶性.
(2)由(I)知F(x)=a•x-4+(a-2)x,分a=0,a=2,a≠0且a≠2三种情况利用定义分别判断函数的奇偶性.
解答:
解:(1)由幂函数f(x)=xm2-2m-3(m∈Z)在(0,+∞)是单调减函数,
得:m2-2m-3<0⇒-1<m<3,又m∈z,∴m=0或1或2,
m=0时f(x)=x-3;m=1时f(x)=x-4,m=2时f(x)=x-3,
又函数是偶函数,∴f(x)=x-4.
(2)F(x)=a•x-4+(a-2)x,
当a=0时,F(x)=-2x,∵F(-x)=-F(x),∴函数是奇函数;
当a=2时,F(x)=
,∵F(-x)=F(x),∴函数是偶函数;
当a≠0且a≠2时,F(1)=2a-2,F(-1)=2,
F(1)≠±F(-1),∴函数对?x∈(-∞,0)∪(0,+∞),F(-x)=F(x)不成立,F(-x)=-F(x)也不成立,
∴函数F(x)是非奇非偶函数.
得:m2-2m-3<0⇒-1<m<3,又m∈z,∴m=0或1或2,
m=0时f(x)=x-3;m=1时f(x)=x-4,m=2时f(x)=x-3,
又函数是偶函数,∴f(x)=x-4.
(2)F(x)=a•x-4+(a-2)x,
当a=0时,F(x)=-2x,∵F(-x)=-F(x),∴函数是奇函数;
当a=2时,F(x)=
| 2 |
| x4 |
当a≠0且a≠2时,F(1)=2a-2,F(-1)=2,
F(1)≠±F(-1),∴函数对?x∈(-∞,0)∪(0,+∞),F(-x)=F(x)不成立,F(-x)=-F(x)也不成立,
∴函数F(x)是非奇非偶函数.
点评:本题考查了幂函数的性质,考查了函数奇偶性的判定,数列掌握幂函数的性质是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
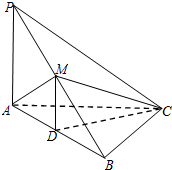 如图,在三棱锥P-ABC中,PA⊥AC,PC⊥BC,M为PB的中点,D为AB的中点,且△AMB为正三角形.
如图,在三棱锥P-ABC中,PA⊥AC,PC⊥BC,M为PB的中点,D为AB的中点,且△AMB为正三角形. 如图,在平行六面体ABCD-A1B1C1D1中,E,H分别是AA1、BB1的中点,求证:
如图,在平行六面体ABCD-A1B1C1D1中,E,H分别是AA1、BB1的中点,求证: