题目内容
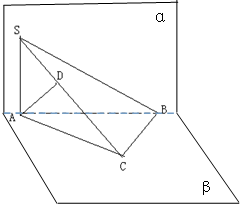 已知直二面角α-AB-β中,S∈平面α,C∈平面β,∠ACB=90°,SA⊥AB,AD⊥SC于D,
已知直二面角α-AB-β中,S∈平面α,C∈平面β,∠ACB=90°,SA⊥AB,AD⊥SC于D,(1)求证:AD⊥平面SBC,
(2)若SA=1,SB=
| 5 |
考点:直线与平面所成的角,直线与平面垂直的判定
专题:空间位置关系与距离
分析:(1)由已知条件,先推导出利用直线与平面垂直的判定理,推导出BC⊥面SAC,从而得到AD⊥BC,由此能够证明AD⊥平面SBC.
(2)由已知条件,过点C作CE⊥面α,交AB于点E,则∠CSE是直线SC与平面α所成角,由此能求出直线SC与平面α所成角的正弦值.
(2)由已知条件,过点C作CE⊥面α,交AB于点E,则∠CSE是直线SC与平面α所成角,由此能求出直线SC与平面α所成角的正弦值.
解答:
解:(1)直二面角α-AB-β中,S∈平面α,C∈平面β,∠ACB=90°,
∵SA⊥AB,AD⊥SC于D,∴SA⊥β,
∵BC?β,∴BC⊥SA,
∵∠ACB=90°,∴AC⊥BC,
∵SA∩AC=A,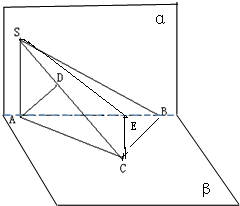 ∴BC⊥面SAC,
∴BC⊥面SAC,
∵AD?面SAC,∴AD⊥BC,
∵AD⊥SC于D,BC∩SC=C,
∴AD⊥平面SBC.
(2)过点C作CE⊥面α,
∵α-AB-β是直二面角,∴E∈AB,
连结SE,则∠CSE是直线SC与平面α所成角,
∵SA=1,SB=
,SA⊥β,∠ACB=90°,
∴AB=
=2,
∵直线SC与平面β所成角为30°,
∴SC=2SA=2,
∴AC=
=
,
∴BC=
=1,
∵S△ABC=
•AC•BC=
•AB•CE
∴CE=
=
,
∴sin∠CSE=
=
=
,
∴直线SC与平面α所成角的正弦值为
.
∵SA⊥AB,AD⊥SC于D,∴SA⊥β,
∵BC?β,∴BC⊥SA,
∵∠ACB=90°,∴AC⊥BC,
∵SA∩AC=A,
 ∴BC⊥面SAC,
∴BC⊥面SAC,∵AD?面SAC,∴AD⊥BC,
∵AD⊥SC于D,BC∩SC=C,
∴AD⊥平面SBC.
(2)过点C作CE⊥面α,
∵α-AB-β是直二面角,∴E∈AB,
连结SE,则∠CSE是直线SC与平面α所成角,
∵SA=1,SB=
| 5 |
∴AB=
| 5-1 |
∵直线SC与平面β所成角为30°,
∴SC=2SA=2,
∴AC=
| 22-12 |
| 3 |
∴BC=
22-(
|
∵S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
∴CE=
| AC•BC |
| AB |
| ||
| 2 |
∴sin∠CSE=
| SE |
| SC |
| ||||
| 2 |
| ||
| 4 |
∴直线SC与平面α所成角的正弦值为
| ||
| 4 |
点评:本题考查直线与平面垂直的证明,考查直线与平面所成角的正弦值的求法,解题时要合理地化空间问题为平面问题.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
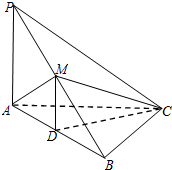 如图,在三棱锥P-ABC中,PA⊥AC,PC⊥BC,M为PB的中点,D为AB的中点,且△AMB为正三角形.
如图,在三棱锥P-ABC中,PA⊥AC,PC⊥BC,M为PB的中点,D为AB的中点,且△AMB为正三角形.