题目内容
已知全集∪=R，设集合A=[-1，+∞），集合B={x|x2+（4-a）x-4a＞0}，若A∩B=A，求实数a的取值范围．
考点：集合的包含关系判断及应用,一元二次不等式的解法
专题：集合
分析：本题的关键是求解集合B，利用A⊆B，求解实数a的取值范围
解答：
解：∵B={x|x2+（4-a）x-4a＞0}，
∴x2+（4-a）x-4a=（x-a）（x+4）
①当a=-4，B=（-∞，-4）∪（-4，+∞），满足A⊆B
②当a＞-4，B=（-∞，-4）∪（a，+∞），若A⊆B，则-4＜a＜-1
③当a＜-4，B=（-∞，a）∪（-4，+∞），若A⊆B，则a＜-4
综上实数a的取值范围，a＜-1
∴x2+（4-a）x-4a=（x-a）（x+4）
①当a=-4，B=（-∞，-4）∪（-4，+∞），满足A⊆B
②当a＞-4，B=（-∞，-4）∪（a，+∞），若A⊆B，则-4＜a＜-1
③当a＜-4，B=（-∞，a）∪（-4，+∞），若A⊆B，则a＜-4
综上实数a的取值范围，a＜-1
点评：题主要考查集合的相等等基本运算，属于基础题．要正确判断两个集合间相等的关系，必须对集合的相关概念有深刻的理解，善于抓住代表元素，认清集合的特征．
练习册系列答案
相关题目
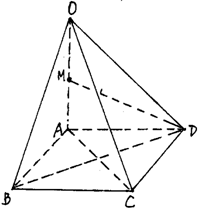如图，在四棱锥O-ABCD中，底面ABCD是边长为1的正方形，OA⊥底面ABCD，OA=2，M为OA中点．
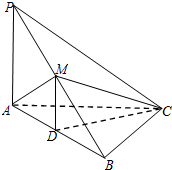如图，在三棱锥P-ABC中，PA⊥AC，PC⊥BC，M为PB的中点，D为AB的中点，且△AMB为正三角形．
如图，在平行六面体ABCD-A1B1C1D1中，E，H分别是AA1、BB1的中点，求证：