题目内容
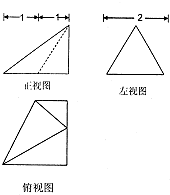若某几何体的三视图（单位：cm）如图所示，其中左视图是一个边长为2的正三角形，则这个几何体的体积是（ ）| A、2cm2 | ||
B、
| ||
C、3
| ||
| D、3cm3 |
考点：由三视图求面积、体积
专题：空间位置关系与距离
分析：由几何体的三视图得到原几何体的底面积与高，进而得到该几何体的体积．
解答：
解：由几何体的三视图可知，该几何体为底面是直角梯形，高为
的四棱锥，
其中直角梯形两底长分别为1和2，高是2．
故这个几何体的体积是
×[
（1+2）×2]×
=
（cm3）．
故选：B．
| 3 |
其中直角梯形两底长分别为1和2，高是2．
故这个几何体的体积是
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| 3 |
故选：B．
点评：本题考查由几何体的三视图求原几何体的体积问题，属于基础题．
练习册系列答案
出彩同步大试卷系列答案
相关题目
已知集合A={x|（
）x＜1}，B={x|x2-3x-4＞0}，则A∩B等于（ ）
| 1 |
| 2 |
| A、{x|x＞0} |
| B、{x|x＜-1或x＞0} |
| C、{x|x＞4} |
| D、{x|-1≤x≤4} |
已知函数f（x）是定义在R上的偶函数，它在[0，+∞）上是减函数．则下列各式一定成立的是（ ）
| A、f（0）＜f（6） |
| B、f（-3）＞f（2） |
| C、f（-1）＞f（3） |
| D、f（-2）＜f（-3） |
某程序框图如图，则该程序运行后输出的值为（ ）
| A、6 | B、7 | C、8 | D、9 |
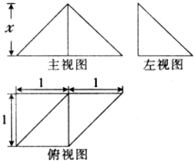如图所示是一个几何体的三视图，若该几何体的体积为| 1 |
| 2 |
A、
| ||
B、
| ||
| C、1 | ||
D、
|