题目内容
某旅行社为调查市民喜欢“人文景观”景点是否与年龄有关,随机抽取了55名市民,得到数据如下表:
(Ⅰ)判断是否有99.5%的把握认为喜欢“人文景观”景点与年龄有关?
(Ⅱ)用分层抽样的方法从喜欢“人文景观”景点的市民中随机抽取6人作进一步调查,将这6位市民作为一个样本,从中任选2人,求恰有1位“大于40岁”的市民和1位“20岁至40岁”的市民的概率.
下面的临界值表供参考:
(参考公式:K2=
,其中n=a+b+c+d)
| 喜欢 | 不喜欢 | 合计 | |
| 大于40岁 | 20 | 5 | 25 |
| 20岁至40岁 | 10 | 20 | 30 |
| 合计 | 30 | 25 | 55 |
(Ⅱ)用分层抽样的方法从喜欢“人文景观”景点的市民中随机抽取6人作进一步调查,将这6位市民作为一个样本,从中任选2人,求恰有1位“大于40岁”的市民和1位“20岁至40岁”的市民的概率.
下面的临界值表供参考:
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
考点:独立性检验的应用
专题:综合题,概率与统计
分析:(Ⅰ)计算K2的值,与临界值比较,即可得到结论;
(II)确定样本中有4个“大于40岁”的市民,2个“20岁至40岁”的市民,利用列举法确定基本事件,即可求得结论.
(II)确定样本中有4个“大于40岁”的市民,2个“20岁至40岁”的市民,利用列举法确定基本事件,即可求得结论.
解答:
解:(1)由公式K2=
≈11.978>7.879,
所以有99.5%的把握认为喜欢“人文景观”景点与年龄有关 …(5分)
(II)设所抽样本中有m个“大于40岁”市民,则
=
,得m=4人
所以样本中有4个“大于40岁”的市民,2个“20岁至40岁”的市民,分别记作B1,B2,B3,B4,G1,G2.
从中任选2人的基本事件有(B1,B2)、(B1,B3)、(B1,B4)、(B1,G1)、(B1,G2)、(B2,B3)、(B2,B4)、(B2,G1)、(B2,G2)、(B3,B4)、(B3,G1)、(B3,G2)、(B4,G1)、(B4,G2)、(G1,G2),共15个,…(9分)
其中恰有1名“大于40岁”和1名“20岁至40岁”之间的市民的事件有(B1,G1)、(B1,G2)、(B2,G1)、(B2,G2)、(B3,G1)、(B3,G2)、(B4,G1)、(B4,G2),共8个,
所以恰有1名“大于40岁”和1名“20岁至40岁”之间的市民的概率为P=
. …(12分)
| 55×(20×20-10×5)2 |
| 30×25×25×30 |
所以有99.5%的把握认为喜欢“人文景观”景点与年龄有关 …(5分)
(II)设所抽样本中有m个“大于40岁”市民,则
| m |
| 20 |
| 6 |
| 30 |
所以样本中有4个“大于40岁”的市民,2个“20岁至40岁”的市民,分别记作B1,B2,B3,B4,G1,G2.
从中任选2人的基本事件有(B1,B2)、(B1,B3)、(B1,B4)、(B1,G1)、(B1,G2)、(B2,B3)、(B2,B4)、(B2,G1)、(B2,G2)、(B3,B4)、(B3,G1)、(B3,G2)、(B4,G1)、(B4,G2)、(G1,G2),共15个,…(9分)
其中恰有1名“大于40岁”和1名“20岁至40岁”之间的市民的事件有(B1,G1)、(B1,G2)、(B2,G1)、(B2,G2)、(B3,G1)、(B3,G2)、(B4,G1)、(B4,G2),共8个,
所以恰有1名“大于40岁”和1名“20岁至40岁”之间的市民的概率为P=
| 8 |
| 15 |
点评:本题考查独立性检验,考查概率知识的运用,考查学生的计算能力,利用列举法确定基本事件是关键.

练习册系列答案
相关题目
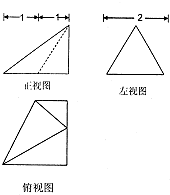 若某几何体的三视图(单位:cm)如图所示,其中左视图是一个边长为2的正三角形,则这个几何体的体积是( )
若某几何体的三视图(单位:cm)如图所示,其中左视图是一个边长为2的正三角形,则这个几何体的体积是( )| A、2cm2 | ||
B、
| ||
C、3
| ||
| D、3cm3 |
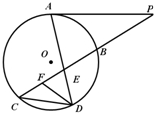 如图所示,已知PA与⊙O相切,A为切点,过点P的割线交圆于B、C两点,弦CD∥AP,AD、BC相交于点E,F为CE上一点,且∠EDF=∠C,若CE:BE=3:2,DE=3,EF=2.则PA=
如图所示,已知PA与⊙O相切,A为切点,过点P的割线交圆于B、C两点,弦CD∥AP,AD、BC相交于点E,F为CE上一点,且∠EDF=∠C,若CE:BE=3:2,DE=3,EF=2.则PA=