题目内容
向面积为S的△ABC内任投一点P，则随机事件“△PBC的面积小于
”的概率为 ．
| S |
| 3 |
考点：几何概型
专题：概率与统计
分析：先求出△PBC的面积等于
时，对应的位置，然后根据几何概型的概率公式求相应的面积，即可得到结论．
| S |
| 3 |
解答：
解：作出△ABC的高AO，当“△PBC的面积等于
”时，此时OP=
AO，
要使“△PBC的面积小于
”，则P位于阴影部分，
则△AEF的面积S1=(
)2S=
S，
则阴影部分的面积为S-
S=
S，
则根据几何概型的概率公式可得“△PBC的面积小于
”的概率为
=
，
故答案为：
．
| S |
| 3 |
| 1 |
| 3 |
要使“△PBC的面积小于
| S |
| 3 |
则△AEF的面积S1=(
| 2 |
| 3 |
| 4 |
| 9 |
则阴影部分的面积为S-
| 4 |
| 9 |
| 5 |
| 9 |
则根据几何概型的概率公式可得“△PBC的面积小于
| S |
| 3 |
| ||
| S |
| 5 |
| 9 |
故答案为：
| 5 |
| 9 |
点评：本题主要考查几何概型的概率公式的计算，根据面积之间的关系是解决本题的关键．
练习册系列答案
相关题目
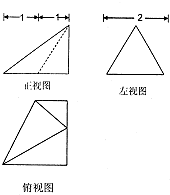若某几何体的三视图（单位：cm）如图所示，其中左视图是一个边长为2的正三角形，则这个几何体的体积是（ ）| A、2cm2 | ||
B、
| ||
C、3
| ||
| D、3cm3 |
为监测幼儿身体发育状况，某幼儿园对“大班”的100名幼儿的体重做了测量，并根据所得数据画出了频率分布直方图，如图所示．则体重在[18，20]（单位kg）的幼儿人数为（ ）