题目内容
已知m为实数,f(x)=2x2-2mx+m-1(0≤m≤2)的最小值记为g(m),试求g(m)的最大值.
考点:二次函数的性质
专题:函数的性质及应用
分析:由已知中函数f(x)的解析式,可得当x=
时,f(x)取最小值-
m2+m-1,即g(m)=-
m2+m-1,再由二次函数的图象和性质,结合m的取值范围,得到g(m)的最大值.
| m |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:f(x)=2x2-2mx+m-1的图象是开口朝上且以直线x=
为对称轴的抛物线,
故当x=
时,f(x)取最小值-
m2+m-1,
即g(m)=-
m2+m-1,
由g(m)的图象是开口朝下且以直线m=1(0≤m≤2)为对称轴的抛物线,
故当m=1时,求g(m)的最大值-
| m |
| 2 |
故当x=
| m |
| 2 |
| 1 |
| 2 |
即g(m)=-
| 1 |
| 2 |
由g(m)的图象是开口朝下且以直线m=1(0≤m≤2)为对称轴的抛物线,
故当m=1时,求g(m)的最大值-
| 1 |
| 2 |
点评:本题考查的知识点是二次函数的性质,熟练掌握二次函数的图象和性质是解答的关键.

练习册系列答案
相关题目
在锐角△ABC中,AB=3,AC=4,其面积S△ABC=3
,则BC=( )
| 3 |
| A、5 | ||||
B、
| ||||
C、
| ||||
D、
|
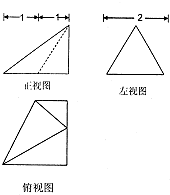 若某几何体的三视图(单位:cm)如图所示,其中左视图是一个边长为2的正三角形,则这个几何体的体积是( )
若某几何体的三视图(单位:cm)如图所示,其中左视图是一个边长为2的正三角形,则这个几何体的体积是( )| A、2cm2 | ||
B、
| ||
C、3
| ||
| D、3cm3 |
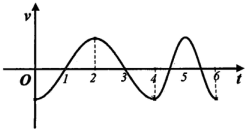
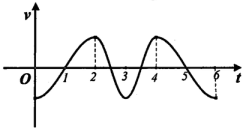
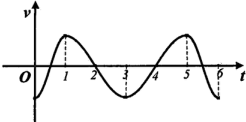
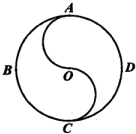 如图,半径为2的圆内有两条半圆弧,一质点M自点A开始沿弧A-B-C-O-A-D-C做匀速运动,则其在水平方向(向右为正)的速度v=v(t)的图象大致为( )
如图,半径为2的圆内有两条半圆弧,一质点M自点A开始沿弧A-B-C-O-A-D-C做匀速运动,则其在水平方向(向右为正)的速度v=v(t)的图象大致为( )