题目内容
已知{an}是递增的等差数列,a1=2,Sn为其前n项和,若a1,a2,a6成等比数列,则S5= .
考点:等比数列的性质,等差数列的前n项和
专题:等差数列与等比数列
分析:由题意设等差数列{an}的公差为d,d>0,由a1,a2,a6成等比数列可得d的方程,解得d代入等差数列的求和公式可得.
解答:
解:由题意设等差数列{an}的公差为d,d>0
∵a1,a2,a6成等比数列,
∴a22=a1•a6,
∴(2+d)2=2(2+5d),
解得d=6,或d=0(舍去)
∴S5=5a1+
d=5×2+10×6=70
故答案为:70
∵a1,a2,a6成等比数列,
∴a22=a1•a6,
∴(2+d)2=2(2+5d),
解得d=6,或d=0(舍去)
∴S5=5a1+
| 5×4 |
| 2 |
故答案为:70
点评:本题考查等差数列和等比数列的综合,求出数列的公差是解决的关键,属基础题.

练习册系列答案
相关题目
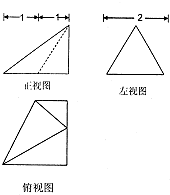 若某几何体的三视图(单位:cm)如图所示,其中左视图是一个边长为2的正三角形,则这个几何体的体积是( )
若某几何体的三视图(单位:cm)如图所示,其中左视图是一个边长为2的正三角形,则这个几何体的体积是( )| A、2cm2 | ||
B、
| ||
C、3
| ||
| D、3cm3 |
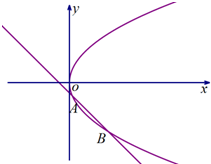 已知抛物线C:y2=4x,直线l:y=-x+b与抛物线C交于A,B两点.
已知抛物线C:y2=4x,直线l:y=-x+b与抛物线C交于A,B两点. 如图,己知
如图,己知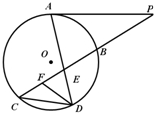 如图所示,已知PA与⊙O相切,A为切点,过点P的割线交圆于B、C两点,弦CD∥AP,AD、BC相交于点E,F为CE上一点,且∠EDF=∠C,若CE:BE=3:2,DE=3,EF=2.则PA=
如图所示,已知PA与⊙O相切,A为切点,过点P的割线交圆于B、C两点,弦CD∥AP,AD、BC相交于点E,F为CE上一点,且∠EDF=∠C,若CE:BE=3:2,DE=3,EF=2.则PA=