题目内容
9.计算:$\lim_{x→1}\frac{{1-\sqrt{x}}}{{1-\root{3}{x}}}$.分析 令$\root{6}{x}=t$,把原式等价转化为$\underset{lim}{t→1}\frac{1+t+{t}^{2}}{1+t}$,由此能求出结果.
解答 解:令$\root{6}{x}=t$,
则$\lim_{x→1}\frac{{1-\sqrt{x}}}{{1-\root{3}{x}}}$=$\underset{lim}{t→1}\frac{1-{t}^{3}}{1-{t}^{2}}$
=$\underset{lim}{t→1}\frac{1+t+{t}^{2}}{1+t}$
=$\frac{1+1+1}{1+1}$
=$\frac{3}{2}$.
点评 本题考查极限值的求法,是基础题,解题时要认真审题,注意换元法的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
20.过直线y=2x上一点P作圆M:${(x-3)^2}+{(y-2)^2}=\frac{4}{5}$的两条切线l1,l2,A,B为切点,当直线l1,l2关于直线y=2x对称时,则∠APB等于( )
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
14.某产品的广告费x(万元)与销售额y(万元)的统计数据如表:
根据如表可知回归直线方程$\stackrel{∧}{y}$=7x+$\stackrel{∧}{a}$,若广告费用为10万元,则预计销售额为73.5万元.
| 广告费x(万元) | 3 | 4 | 5 | 6 |
| 销售额y(万元) | 25 | 30 | 40 | 45 |
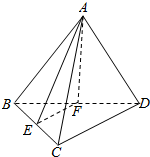 如图,正三棱锥A-BCD的侧棱长为2,底面BCD的边长为2$\sqrt{2}$,E,分别为BC,BD的中点,则三棱锥A-BEF的外接球的半径R=1,内切球半径r=2-$\sqrt{3}$.
如图,正三棱锥A-BCD的侧棱长为2,底面BCD的边长为2$\sqrt{2}$,E,分别为BC,BD的中点,则三棱锥A-BEF的外接球的半径R=1,内切球半径r=2-$\sqrt{3}$.