题目内容
4．解关于x的不等式：ax2-x+1＜0．分析 利用一元二次不等式的性质根据a的取值进行分类讨论，由此能求出原不等式的解集．
解答 解：∵ax2-x+1＜0，
∴当a=0时，-x+1＜0，解得x＞1，原不等式解集为{x|x＞1}．
当a＜0时，-ax2+x-1＞0，
当△=1-4a=0，即a=$\frac{1}{4}$时，不满足a＜0，故无解；
当△=1-4a＞0时，a＜$\frac{1}{4}$，解方程-ax2+x-1=0，得x=$\frac{-1±\sqrt{1-4a}}{-2a}$，
∴原不等式的解集为：{x|x＜$\frac{1+\sqrt{1-4a}}{2a}$}；
当△=1-4a＜0，即a＞$\frac{1}{4}$，不满足a＜0，故无解；
当a＞0时，ax2-x+1＜0
当△=1-4a=0，即a=$\frac{1}{4}$时，原不等式的解集为{x|x≠$\frac{1}{2a}$}；
当△=1-4a＞0时，0＜a＜$\frac{1}{4}$，解方程ax2-x+1=0，得x=$\frac{1±\sqrt{1-4a}}{2a}$，
∴原不等式的解集为：{x|$\frac{1-\sqrt{1-4a}}{2a}$＜x＜$\frac{1+\sqrt{1-4a}}{2a}$}；
当△=1-4a＜0，即a＞$\frac{1}{4}$，原不等式的解集为R．
点评 本题考查一元二次不等式的解法，是中档题，解题时要认真审题，注意分类讨论思想的合理运用．
练习册系列答案
阅读快车系列答案
相关题目
14．
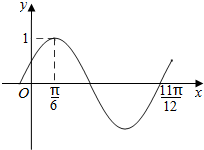函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示，若将y=f（x）的图象向右平移m（m＞0）个单位后，得到的图象关于原点对称，则m的最小值为（ ）
函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示，若将y=f（x）的图象向右平移m（m＞0）个单位后，得到的图象关于原点对称，则m的最小值为（ ）| A． | $\frac{π}{24}$ | B． | $\frac{π}{12}$ | C． | $\frac{π}{6}$ | D． | $\frac{π}{3}$ |
19．设f0（x）=sinx，f1（x）=f0′（x），f2（x）=f1′（x），…，fn+1（x）=fn′（x），n∈N，则f2016（x）=（ ）
| A． | sinx | B． | -sinx | C． | cosx | D． | -cosx |
