题目内容
19.函数$y={(\frac{1}{2})^x}-1$在区间[-2,1]上的值域为[-$\frac{1}{2}$,3].分析 根据指数函数的单调性,求出该函数在区间[-2,1]上的最值即可.
解答 解:函数$y={(\frac{1}{2})^x}-1$在定义域R上是单调减函数,
且在区间[-2,1]上的最大值为${(\frac{1}{2})}^{-2}$-1=3,
最小值是$\frac{1}{2}$-1=-$\frac{1}{2}$;
所以该函数在区间[-2,1]上的值域为[-$\frac{1}{2}$,3].
故答案为:[-$\frac{1}{2}$,3].
点评 本题考查了根据函数的单调性求指数函数在闭区间上最值和值域的应用问题,是基础题目.

练习册系列答案
相关题目
7.已知f(x)=ax2+bx+1是定义在[-2a,a2-3]上的偶函数,那么a+b的值是( )
| A. | 3 | B. | -1 | C. | -1或3 | D. | 1 |
14.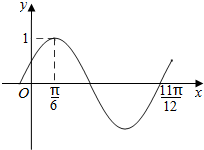 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,若将y=f(x)的图象向右平移m(m>0)个单位后,得到的图象关于原点对称,则m的最小值为( )
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,若将y=f(x)的图象向右平移m(m>0)个单位后,得到的图象关于原点对称,则m的最小值为( )
 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,若将y=f(x)的图象向右平移m(m>0)个单位后,得到的图象关于原点对称,则m的最小值为( )
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,若将y=f(x)的图象向右平移m(m>0)个单位后,得到的图象关于原点对称,则m的最小值为( )| A. | $\frac{π}{24}$ | B. | $\frac{π}{12}$ | C. | $\frac{π}{6}$ | D. | $\frac{π}{3}$ |
8.为了解少年儿童的肥胖是否与常喝碳酸饮料有关,现对30名六年级学生进行了问卷调查,得到如下2×2列联表,平均每天喝500ml以上为常喝,体重超过50kg为肥胖.
已知在这30人中随机抽取1人,抽到肥胖的学生的概率为$\frac{4}{15}$.
(1)请将上面的列联表补充完整.
(2)是否有99.5%的把握认为肥胖与常喝碳酸饮料有关?说明你的理由.
参考数据:
参考公式:K2=$\frac{n(ad-cb)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d.
| 常喝 | 不常喝 | 合计 | |
| 肥胖 | 2 | ||
| 不肥胖 | 18 | ||
| 合计 | 30 |
(1)请将上面的列联表补充完整.
(2)是否有99.5%的把握认为肥胖与常喝碳酸饮料有关?说明你的理由.
参考数据:
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
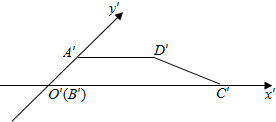 已知梯形ABCD是直角梯形,按照斜二测画法画出它的直观图A′B′C′D′(如图所示),其中A′D′=2,B′C′=4,A′B′=1,则直角梯形DC边的长度是2$\sqrt{2}$.
已知梯形ABCD是直角梯形,按照斜二测画法画出它的直观图A′B′C′D′(如图所示),其中A′D′=2,B′C′=4,A′B′=1,则直角梯形DC边的长度是2$\sqrt{2}$.