题目内容
20.过直线y=2x上一点P作圆M:${(x-3)^2}+{(y-2)^2}=\frac{4}{5}$的两条切线l1,l2,A,B为切点,当直线l1,l2关于直线y=2x对称时,则∠APB等于( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
分析 连接PM、AM,根据圆的性质和轴对称知识,得当切线l1,l2关于直线l对称时,直线l⊥PM,且PM平分∠APB.因此计算出圆的半径和点M到直线l的距离,在Rt△PAM中利用三角函数定义算出∠APM的度数,从而得到∠APB的度数.
解答  解:连接PM、AM,可得当切线l1,l2关于直线l对称时,
解:连接PM、AM,可得当切线l1,l2关于直线l对称时,
直线l⊥PM,且射线PM恰好是∠APB的平分线,
∵圆M的方程为(x-3)2+(y-2)2=$\frac{4}{5}$,
∴点M坐标为(3,2),半径r=$\frac{2\sqrt{5}}{5}$,
点M到直线l:2x-y=0的距离为PM=$\frac{|2×3-2|}{\sqrt{{2}^{2}+(-1)^{2}}}$=$\frac{4\sqrt{5}}{5}$,
由PA切圆M于A,得Rt△PAM中,sin∠APM=$\frac{AM}{PM}$=$\frac{1}{2}$,
得∠APM=30°,
∴∠APB=2∠APM=60°.
故选:C.
点评 本题在直角坐标系中给出圆的两条切线关于已知直线对称,求它们之间所成的角,着重考查了圆的标准方程、点到直线的距离、直线与圆的位置关系和轴对称等知识,属于中档题.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
8.为了解少年儿童的肥胖是否与常喝碳酸饮料有关,现对30名六年级学生进行了问卷调查,得到如下2×2列联表,平均每天喝500ml以上为常喝,体重超过50kg为肥胖.
已知在这30人中随机抽取1人,抽到肥胖的学生的概率为$\frac{4}{15}$.
(1)请将上面的列联表补充完整.
(2)是否有99.5%的把握认为肥胖与常喝碳酸饮料有关?说明你的理由.
参考数据:
参考公式:K2=$\frac{n(ad-cb)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d.
| 常喝 | 不常喝 | 合计 | |
| 肥胖 | 2 | ||
| 不肥胖 | 18 | ||
| 合计 | 30 |
(1)请将上面的列联表补充完整.
(2)是否有99.5%的把握认为肥胖与常喝碳酸饮料有关?说明你的理由.
参考数据:
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
5.设全集U={-2,-1,0,1,2},集合A={x|x2-x-2=0},B={1,2},则(∁UA)∪B=( )
| A. | {-2,-1,0,1,2} | B. | {-2,0,1,2} | C. | {-1,2} | D. | {-1,1,2} |
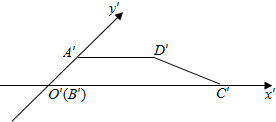 已知梯形ABCD是直角梯形,按照斜二测画法画出它的直观图A′B′C′D′(如图所示),其中A′D′=2,B′C′=4,A′B′=1,则直角梯形DC边的长度是2$\sqrt{2}$.
已知梯形ABCD是直角梯形,按照斜二测画法画出它的直观图A′B′C′D′(如图所示),其中A′D′=2,B′C′=4,A′B′=1,则直角梯形DC边的长度是2$\sqrt{2}$.