题目内容
16．某四棱锥和球的组合体的三视图如图所示，则该组合体的体积是$\frac{8+4π}{3}$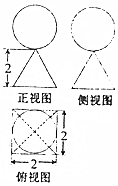
分析 由三视图可得该组合体为上面为球，下面为正四棱锥组成，球的半径为1，正四棱锥的底面边长为2，高为2，运用球的体积公式和棱锥的体积公式，计算即可得到所求．
解答 
解：该组合体由上面为球，下面为正四棱锥组成，
球的半径为1，正四棱锥的底面边长为2，高为2，
则该组合体的体积是$\frac{4}{3}$π•13+$\frac{1}{3}$•22•2=$\frac{8+4π}{3}$．
故答案为：$\frac{8+4π}{3}$．
点评 本题考查组合体的体积的求法，注意运用球的体积公式和棱锥的体积公式，由三视图正确还原几何体的直观图是解题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
4．若$sinα+3sin（\frac{π}{2}+α）=0$，则cos2α的值为（ ）
| A． | $-\frac{3}{5}$ | B． | $\frac{3}{5}$ | C． | $-\frac{4}{5}$ | D． | $\frac{4}{5}$ |
11．“共享单车”的出现，为我们提供了一种新型的交通方式．某机构为了调查人们对此种交通方式的满意度，从交通拥堵不严重的A城市和交通拥堵严重的B城市分别随机调查了20个用户，得到了一个用户满意度评分的样本，并绘制出茎叶图如图：
（Ⅰ）根据茎叶图，比较两城市满意度评分的平均值的大小及方差的大小（不要求计算出具体值，给出结论即可）；
（Ⅱ）若得分不低于80分，则认为该用户对此种交通方式“认可”，否则认为该用户对此种交通方式“不认可”，请根据此样本完成此2×2列联表，并据此样本分析是否有95%的把握认为城市拥堵与认可共享单车有关；
（Ⅲ）若从此样本中的A城市和B城市各抽取1人，则在此2人中恰有一人认可的条件下，此人来自B城市的概率是多少？
附：参考数据：
（参考公式：${Χ^2}=\frac{{n{{（{n_{11}}{n_{22}}-{n_{12}}{n_{21}}）}^2}}}{{{n_{1+}}{n_{2+}}{n_{+1}}{n_{+2}}}}$）
（Ⅰ）根据茎叶图，比较两城市满意度评分的平均值的大小及方差的大小（不要求计算出具体值，给出结论即可）；
（Ⅱ）若得分不低于80分，则认为该用户对此种交通方式“认可”，否则认为该用户对此种交通方式“不认可”，请根据此样本完成此2×2列联表，并据此样本分析是否有95%的把握认为城市拥堵与认可共享单车有关；
| A | B | 合计 | |
| 认可 | |||
| 不认可 | |||
| 合计 |
附：参考数据：
（参考公式：${Χ^2}=\frac{{n{{（{n_{11}}{n_{22}}-{n_{12}}{n_{21}}）}^2}}}{{{n_{1+}}{n_{2+}}{n_{+1}}{n_{+2}}}}$）
1．已知函数f（x）=sinx+cosx，g（x）=2cosx，动直线x=t与f（x）和g（x）的图象分别交于A、B两点，则|AB|的取值范围是（ ）
| A． | [0，1] | B． | [0，$\sqrt{2}$] | C． | [0，2] | D． | [1，$\sqrt{2}$] |
5．现有A，B两门选修课供甲、乙、丙三人随机选择，每人必须且只能选其中一门，则甲乙两人都选A选修课的概率是（ ）
| A． | $\frac{1}{4}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{2}$ | D． | $\frac{2}{3}$ |
20．A={x|y=lg（x-1）}，$B=\left\{{y\left|{y=\sqrt{4-{x^2}}}\right.}\right\}$，则A∩B=（ ）
| A． | [0，2] | B． | （1，2] | C． | [1，2） | D． | （1，4] |