题目内容
证明：函数f（x）=
在区间（0，2）上是单调递增函数．
| lnx |
| x |
考点：利用导数研究函数的单调性
专题：导数的概念及应用
分析：求出函数f（x） 的导数为y′的解析式，令y′＞0 求得x的范围，即可得到函数f（x）的单调递增区间，然后可说明函数在区间（0，2）上是单调递增函数．
解答：
证明：由于函数f（x）=
的导数为y′=
，
令y′＞0 可得 lnx＜1，解得0＜x＜e，
故函数f（x）的单调递增区间是 （0，e），
又∵区间（0，2）?（0，e），
∴函数f（x）=
在区间（0，2）上是单调递增函数．
| lnx |
| x |
| 1-lnx |
| x2 |
令y′＞0 可得 lnx＜1，解得0＜x＜e，
故函数f（x）的单调递增区间是 （0，e），
又∵区间（0，2）?（0，e），
∴函数f（x）=
| lnx |
| x |
点评：本题主要考查利用导数研究函数的单调性，导数的求导法则，要熟记属于中档题目．
练习册系列答案
期末好成绩系列答案
99加1领先期末特训卷系列答案
百强名校期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案
金状元绩优好卷系列答案
相关题目
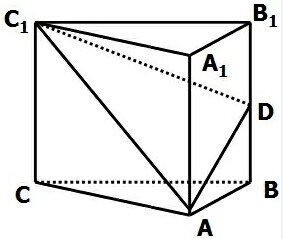直三棱柱ABC-A1B1C1中，A1A=AC=
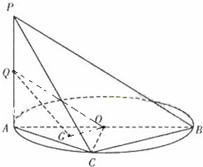如图，AB是⊙O的直径，PA垂直于⊙O所在的平面，C是圆上的点．