题目内容
使得抛物线上y2=4x上一点M到点A（
，-2）与到焦点的距离之和最小，则点M的坐标为 ．
| 5 |
| 2 |
考点：两点间的距离公式
专题：圆锥曲线的定义、性质与方程
分析：过点A作AE⊥l，垂足为E．则|ME|=|MF|．因此当三点A，M，E共线时，|AM|+|ME|=|BE|取得最小值，由此能求出结果．
解答：
解：由抛物线y2=4x，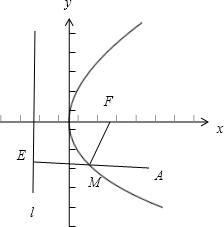
得焦点F（1，0），准线l的方程：x=-1．
如图所示，过点A作AE⊥l，垂足为E．则|ME|=|MF|．
因此当三点A，M，E共线时，
|AM|+|ME|=|BE|取得最小值
-（-1）=
．
此时yM=-2，代入抛物线方程可得（-2）2=4xM，解得xM=1．
∴点M（1，-2）．
故答案为：（1，-2）．
得焦点F（1，0），准线l的方程：x=-1．
如图所示，过点A作AE⊥l，垂足为E．则|ME|=|MF|．
因此当三点A，M，E共线时，
|AM|+|ME|=|BE|取得最小值
| 5 |
| 2 |
| 7 |
| 2 |
此时yM=-2，代入抛物线方程可得（-2）2=4xM，解得xM=1．
∴点M（1，-2）．
故答案为：（1，-2）．
点评：本题考查满足条件的点的坐标的求法，是中档题，解题时要认真审题，注意抛物线性质的合理运用．
练习册系列答案
相关题目
函数y=
（ ）
| ex-e-x |
| 2 |
| A、是奇函数，它在R上是减函数 |
| B、是偶函数，它在R上是减函数 |
| C、是奇函数，它在R上是增函数 |
| D、是偶函数，它在R上是增函数 |
（1）说明由函数y=log3（x-1）作怎样的变换可以得到函数y=log3（x+2）的图象；设集合M={1，2，3}，N={1，3}，则下列关系正确的是（ ）
| A、N∈M | B、N∉M |
| C、N=M | D、N?M |