Question

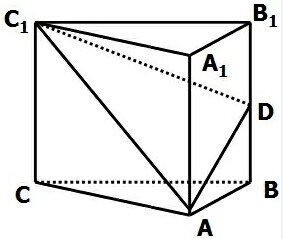直三棱柱ABC-A₁B₁C₁中，A₁A=AC=

2

AB，AB=BC=a，D为BB₁的中点．
（1）证明：平面ADC₁⊥AA₁C₁C；
（2）求点B到平面ADC₁的距离．

Answer 1

考点：点、线、面间的距离计算,平面与平面垂直的判定

专题：空间位置关系与距离

分析：（1）首先利用线面垂直的性质得到线线垂直，进一步利用线线垂直转化成线面垂直，最后转化成面面垂直．
（2）利用（1）的结论解出相关的线段长，进一步利用体积相等求出结果．

解答： （1）证明：直三棱柱ABC-A₁B₁C₁中，A₁A=AC=

2

a，AB=BC=a，D为BB₁的中点．
所以：AB⊥BC
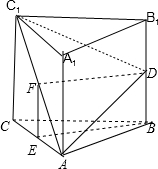
取AC的中点E，AC₁的中点F，连接BE，DF．
所以：DF∥BE
由于：在直三棱柱ABC-A₁B₁C₁中，BE⊥AC，BE⊥CC₁
所以：BE⊥平面AA₁C₁C．
由于DF∥BE
DF⊥平面AA₁C₁C．
DF?平面ADC₁
所以：平面ADC₁⊥AA₁C₁C；
（2）根据（1）的结论DF⊥平面AA₁C₁C．
所以：DF=BE=

2

2

a，AC₁=2a
S△ADC1=

1

2

•2a•

2

2

a
S△ABD=

1

2

•a•

2

2

a
利用VB-ADC1=VC-ABD
设点B到平面ADC₁的距离为h．

1

3

•

2

2

a•

1

2

•2a•h=

1

3

•

a

2

•

2

2

a•a
解得：h=

a

2

点评：本题考查的知识要点：线面垂直的判定和性质定理，锥体的体积公式的应用及相关的运算问题．属于基础题型．