题目内容
 如图,在直角梯形ABCD中,AB∥CD,AB⊥BC,AB=2,CD=1,BC=2,P为线段AD(含端点)上一个动点.设
如图,在直角梯形ABCD中,AB∥CD,AB⊥BC,AB=2,CD=1,BC=2,P为线段AD(含端点)上一个动点.设| AP |
| AD |
| PB |
| PC |
考点:函数解析式的求解及常用方法,平面向量数量积的运算
专题:函数的性质及应用,平面向量及应用
分析:画出图形,建立直角坐标系,设出点P的坐标,表示出
、
、
、
;求出
•
的值,即得y=f(x)的解析式;求出y的最值,即得f(x)的值域.
| AP |
| AD |
| PB |
| PC |
| PB |
| PC |
解答:
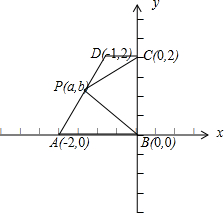 解:如图,建立直角坐标系;
解:如图,建立直角坐标系;
设点P(a,b),则-2≤a≤-1;
∴
=(a+2,b),
=(1,2);
=(-a,-b),
=(-a,2-b);
又∵
=x
,
∴
,
即
,(其中0≤x≤1);
∴
•
=(-a,-b)•(-a,2-b)
=a2-b(2-b)
=(x-2)2-2x•(2-2x)
=5x2-8x+4;
即y=f(x)=5x2-8x+4,其中0≤x≤1;
∴当x=1时,y=f(1)=5-8+4=1;
当x=-
=
时,y取得最小值f(
)=
,
当x=0时,y取得最大值f(0)=4;
∴f(x)的值域是[
,4].
故答案为:1,[
,4].
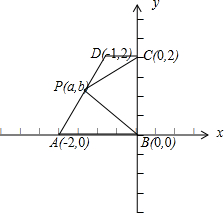 解:如图,建立直角坐标系;
解:如图,建立直角坐标系;设点P(a,b),则-2≤a≤-1;
∴
| AP |
| AD |
| PB |
| PC |
又∵
| AP |
| AD |
∴
|
即
|
∴
| PB |
| PC |
=a2-b(2-b)
=(x-2)2-2x•(2-2x)
=5x2-8x+4;
即y=f(x)=5x2-8x+4,其中0≤x≤1;
∴当x=1时,y=f(1)=5-8+4=1;
当x=-
| -8 |
| 2×5 |
| 4 |
| 5 |
| 4 |
| 5 |
| 4 |
| 5 |
当x=0时,y取得最大值f(0)=4;
∴f(x)的值域是[
| 4 |
| 5 |
故答案为:1,[
| 4 |
| 5 |
点评:本题考查了平面向量的应用以及函数解析式的求法和求函数的值域问题,解题时应建立直角坐标系,结合图形解答问题,是综合题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
以下有关命题的说法错误的是( )
| A、命题“若x2-3x+2=0,则x=1”的逆否命题为“若x≠1,则x2-3x+2≠0” | ||||||
B、“cosα=-
| ||||||
| C、对于命题p:?x∈R,使得x2+x+1<0,则¬p:?x∈R,则x2+x+1≥0 | ||||||
| D、若p∧q为假命题,则p、q均为假命题 | ||||||
| E、对于命题p:?x∈R,使得x2+x+1<0,则¬p:?x∈R,则x2+x+1≥0 |