题目内容
一束光线l自A(1,0)发出,射到直线m:x+y+1=0上,被直线m反射到圆x2+y2-6x-2y+9=0上的点B.
(1)当反射线通过圆心C时,求入射光线l的方程;
(2)求光线由A到达B的最短路径的长.

(1)当反射线通过圆心C时,求入射光线l的方程;
(2)求光线由A到达B的最短路径的长.
考点:与直线关于点、直线对称的直线方程
专题:计算题,直线与圆
分析:(1)由题意,利用物理的光学知识可知入射光线上的任意一点关于直线m对称的点必在其反射线上,由于反射线过圆心,有光线的可逆性知,反射线上的圆心关于直线m对称的点也必在入射光线上,然后由入射光线上已知两点写出所求的直线方程;
(2)设A关于直线m的对称点为A',求出对称点,由对称性可知,所求光线传播到圆的路径长,要使得其最小,则A'B过圆心C时满足条件,根据两点间的距离公式可求.
(2)设A关于直线m的对称点为A',求出对称点,由对称性可知,所求光线传播到圆的路径长,要使得其最小,则A'B过圆心C时满足条件,根据两点间的距离公式可求.
解答:
解:(1)⊙C:(x-3)2+(y-1)2=1,C(3,1),r=1.
设C关于直线m:x+y+1=0的对称点C′(m,n),
即有
,解得,
.
则C'(-2,-4),
即有过A,C′的方程:4x-3y-4=0即为光线l的方程.
(2)光线由A到达B的路程,要想最短,则反射光线必经过圆心,
设A关于直线m:x+y+1=0的对称点A′(a,b),
则
,解得,
,
可得A'(-1,-2),则连接A'C,交圆于B,A'B即为最短路程.
|A'B|=|A'C|-r=
-1=5-1=4.
故光线由A到达B的最短路径的长为4.
设C关于直线m:x+y+1=0的对称点C′(m,n),
即有
|
|
则C'(-2,-4),
即有过A,C′的方程:4x-3y-4=0即为光线l的方程.
(2)光线由A到达B的路程,要想最短,则反射光线必经过圆心,
设A关于直线m:x+y+1=0的对称点A′(a,b),
则
|
|
可得A'(-1,-2),则连接A'C,交圆于B,A'B即为最短路程.
|A'B|=|A'C|-r=
| (3+1)2+(1+2)2 |
故光线由A到达B的最短路径的长为4.
点评:本题考查点关于直线的对称,考查直线方程的求法,以及直线与圆的位置关系,考查运算能力,属于中档题.

练习册系列答案
相关题目
某几何体的三视图如图所示,则它的体积为( )
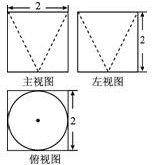

A、8-
| ||
B、8-
| ||
| C、8-2π | ||
D、
|
棱长为1的正方体ABCD-A1B1C1D1中,点P1,P2分别是线段AB,BD1(不包括端点上的动点,且线段P1P2平行于平面A1ADD1,则四面体P1P2AB1的体积的最大值是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
函数f(x)=x2+(m2+2)+m在(-1,1)上零点的个数为( )
| A、1 | B、2 | C、0 | D、不能确定 |

 如图是自治区环境监测网从8月21日至25日五天监测到甲城市和乙城市的空气质量指数数据,用茎叶图表示:
如图是自治区环境监测网从8月21日至25日五天监测到甲城市和乙城市的空气质量指数数据,用茎叶图表示: