题目内容
设A，B分别为关于x的不等式x2-mx+4m-1＜0与
＜0的解集，若A?B，则m的取值范围是 ．
| x+1 |
| x-3 |
考点：其他不等式的解法
专题：不等式的解法及应用
分析：求出分式不等式的交集得到集合B，利用二次不等式与二次函数根的分布，列出m的关系式，求出m的范围即可．
解答：
解：由
＜0可得x∈（-1，3）．
不等式x2-mx+4m-1＜0，对应的函数为f（x）=x2-mx+4m-1．
∵A?B，
∴
，即：
，
解得m≤-8．
故答案为：（-∞，-8]．
| x+1 |
| x-3 |
不等式x2-mx+4m-1＜0，对应的函数为f（x）=x2-mx+4m-1．
∵A?B，
∴
|
|
解得m≤-8．
故答案为：（-∞，-8]．
点评：本题考查分式不等式的求法，二次函数与二次不等式的关系的应用，根的分布的应用，考查转化思想计算能力．
练习册系列答案
相关题目
某空间几何体的三视图如图所示，则该几何体的体积为（ ）
| A、1200+72π |
| B、B、1200+144π |
| C、1600+72π |
| D、1600+144π |
在区间（-∞，0）上为增函数的是（ ）
| A、y=-2x | ||
B、y=
| ||
| C、y=-x2 | ||
| D、y=|x| |
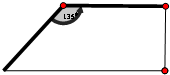两直立矮墙成135°二面角，现利用这两面矮墙和篱笆围成一个面积为54m2的直角梯形菜园（墙足够长），已知修筑篱笆每米的费用为50元，则修筑这个菜园的最少费用为为