题目内容

若函数y=x2-kx+k2-k-2的两个零点分别在区间（0，1），（1，2），求k的取值范围．
考点：一元二次方程的根的分布与系数的关系
专题：函数的性质及应用
分析：由f（x）的图象与x轴的两个交点分别在开区间（0，1）与（1，2）上，则
f(0)＞0
f(1)＜0
f(2)＞0
，解不等式即可求出实数k的取值范围．
解答： 解：由y=x2-kx+k2-k-2的图象开口向上，且与x轴的两个交点分别在开区间（0，1）与（1，2）上，
则
f(0)＞0
f(1)＜0
f(2)＞0
，
即
k2-k-2＞0
k2-2k-1＜0
k2-3k+2＞0

解得：k∈（1-
2
，1）
点评：本题主要考查了二次函数的实根分布问题的应用，解题的关键是灵活利用二次函数的图象及结合图象的性质进行求解，属于中档试题．
练习册系列答案
相关题目
下列四个命题中，真命题的个数有（　　）
①若a，b，c∈R，则“ac2＞bc2”是“a＞b”成立的充分必要条件；
②命题“?x∈R使得x2+x+1＞0的否定是“?x∈R均有x2+x+1≤0”；
③命题“若|x|≥2，则x≥2或x≤-2”的否命题是“若|x|＜2，则-2＜x＜2”；
④函数f（x）=lnx+x-
3
2
在区间（1，2）上有且仅有一个零点．
A、1个B、2个C、3个D、4个
如图，在四棱锥P-ABCD中，BC⊥平面PAB，且PA=P，O是AB的中点，底面ABCD是直角梯形，AD∥BC，BC=1，AB=2，AD=3．
（1）求证：平面PAC⊥平面POC；
（2）若PA=3，Q是PB的中点，求三棱锥Q-OBC与三棱锥P-OCD的体积比．
一束光线l自A（1，0）发出，射到直线m：x+y+1=0上，被直线m反射到圆x2+y2-6x-2y+9=0上的点B．
（1）当反射线通过圆心C时，求入射光线l的方程；
（2）求光线由A到达B的最短路径的长．
下列说法，其中正确命题的序号为
 
．
①若函数f（x）=x（x-c）2在x=2处有极大值，则c=2实数或6；
②对于R上可导的任意函数f（x），若满足（x-1）f′（x）≥0，则必有f（0）+f（2）＞2f（1）；
③若函数f（x）=x3-3x在（a2-17，a）上有最大值，则实数a的取值范围为（-1，4）；
④已知函数f（x）是定义在R上的奇函数f（1）=0，xf′（x）-f（x）＞0（x＞0），则不等式f（x）＞0的解集是（-1，0）∪（1，+∞）．
已知f（x）为定义在R上的偶函数，x≥0时，f（x）=x2-4x+3．
（1）求x＜0时函数的解析式；
（2）在给出的直角坐标系中画出y=f（x）的图象，并写出f（x）的单调递增区间；
（3）求函数f（x）在[0，3]的最大值及最小值．
已知函数f（x）=ex-ax，其中e为自然对数的底数，a为常数．
（1）若对函数f（x）存在极小值，且极小值为0，求a的值；
（2）若对任意x∈[0，
π
2
]，不等式f（x）≥ex（1-sinx）恒成立，求a的取值范围．
某空间几何体的三视图如图所示，则该几何体的体积为（　　）
A、1200+72π
B、B、1200+144π
C、1600+72π
D、1600+144π
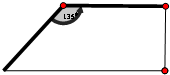两直立矮墙成135°二面角，现利用这两面矮墙和篱笆围成一个面积为54m2的直角梯形菜园（墙足够长），已知修筑篱笆每米的费用为50元，则修筑这个菜园的最少费用为为
 
元．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网