题目内容
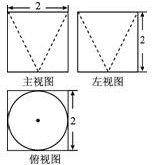
某几何体的三视图如图所示，则它的体积为（ ）
A、8-
| ||
B、8-
| ||
| C、8-2π | ||
D、
|
考点：由三视图求面积、体积
专题：计算题,空间位置关系与距离
分析：三视图中长对正，高对齐，宽相等；由三视图想象出直观图，一般需从俯视图构建直观图，该几何体为正方体内挖去一个圆锥．
解答：
解：由题意可知，该几何体为正方体内挖去一个圆锥，
正方体的边长为2，圆锥的底面半径为1，高为2，
则正方体的体积为V1=23=8，圆锥的体积为V2=
•π•12•2=
，
则该几何体的体积为V=8-
，
故选A．
正方体的边长为2，圆锥的底面半径为1，高为2，
则正方体的体积为V1=23=8，圆锥的体积为V2=
| 1 |
| 3 |
| 2π |
| 3 |
则该几何体的体积为V=8-
| 2π |
| 3 |
故选A．
点评：三视图中长对正，高对齐，宽相等；由三视图想象出直观图，一般需从俯视图构建直观图，本题考查了学生的空间想象力，识图能力及计算能力．
练习册系列答案
名校课堂系列答案
相关题目
已知集合A={y|y=
，x＞0}，B={x|y=ln（2x-4）}，若m∈A，m∉B，则实数m的取值范围是（ ）
| 1 |
| x |
| A、（-∞，0） |
| B、（2，+∞） |
| C、（0，2） |
| D、（0，2] |
如图所示，在三棱锥P-ABC中，E、F分别为AC、BC的中点．