题目内容
已知数列{an}满足an+1=3an+2,n∈N*,a1=1,bn=an+1
(1)证明数列{bn}为等比数列.
(2)求数列{an}的通项公式an与前n项和Sn.
(1)证明数列{bn}为等比数列.
(2)求数列{an}的通项公式an与前n项和Sn.
考点:数列递推式,数列的求和
专题:等差数列与等比数列
分析:(1)由已知得an+1+1=3(an+1),又a1=1,bn=an+1,由此能证明数列{bn}为首项为2,公比为3的等比数列.
(2)由(1)知an+1=2×3n-1,由此能求出数列{an}的通项公式an与前n项和Sn.
(2)由(1)知an+1=2×3n-1,由此能求出数列{an}的通项公式an与前n项和Sn.
解答:
(1)证明:∵an+1=3an+2,n∈N*,a1=1,
∴an+1+1=3(an+1),又a1=1,bn=an+1
∴
=
=3,
∴数列{bn}为首项为2,公比为3的等比数列.
(2)解:由(1)知an+1=2×3n-1,∴an=2×3n-1-1.
∴Sn=2×(1+3+32+…+3n-1)-n
=2×
-n
=3n-n-1.
∴an+1+1=3(an+1),又a1=1,bn=an+1
∴
| bn+1 |
| bn |
| an+1+1 |
| an+1 |
∴数列{bn}为首项为2,公比为3的等比数列.
(2)解:由(1)知an+1=2×3n-1,∴an=2×3n-1-1.
∴Sn=2×(1+3+32+…+3n-1)-n
=2×
| 1×(1-3n) |
| 1-3 |
=3n-n-1.
点评:本题考查等比数列的证明,考查数列的通项公式和前n项和的求法,是中档题,解题时要认真审题,注意等比数列的性质的合理运用.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
在区间(-∞,0)上为增函数的是( )
| A、y=-2x | ||
B、y=
| ||
| C、y=-x2 | ||
| D、y=|x| |
 如图,在四棱锥P-ABCD中,BC⊥平面PAB,且PA=P,O是AB的中点,底面ABCD是直角梯形,AD∥BC,BC=1,AB=2,AD=3.
如图,在四棱锥P-ABCD中,BC⊥平面PAB,且PA=P,O是AB的中点,底面ABCD是直角梯形,AD∥BC,BC=1,AB=2,AD=3.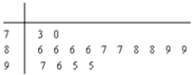 某电视台组织部分记者,用“10分制”随机调查某社区居民的幸福指数,现从调查人群中随机抽取16名,如图所示的茎叶图记录了他们的幸福指数的得分(以小数点前的一位数字为茎,小数点后的一位数字为叶):
某电视台组织部分记者,用“10分制”随机调查某社区居民的幸福指数,现从调查人群中随机抽取16名,如图所示的茎叶图记录了他们的幸福指数的得分(以小数点前的一位数字为茎,小数点后的一位数字为叶):