Question

棱长为1的正方体ABCD-A₁B₁C₁D₁中，点P₁，P₂分别是线段AB，BD₁（不包括端点上的动点，且线段P₁P₂平行于平面A₁ADD₁，则四面体P₁P₂AB₁的体积的最大值是（　　）

• A、

  1

  24

• B、

  1

  12

• C、

  1

  6

• D、

  1

  2

Answer 1

考点：棱柱、棱锥、棱台的体积

专题：计算题,空间位置关系与距离

分析：由题意可得△P₁P₂B∽△AD₁B，设出P₁B=x，则P₁P₂=

2

x，P₂到平面AA₁B₁B的距离为x，求出四面体的体积，通过二次函数的最值，求出四面体的体积的最大值．

解答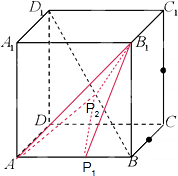： 解：由题意在棱长为1的正方体ABCD-A₁B₁C₁D₁中，点P₁，P₂分别是线段AB，BD₁（不包括端点）上的动点，且线段P₁P₂平行于平面A₁ADD₁，△P₁P₂B∽△AD₁B，
设P₁B=x，x∈（0，1），则P₁P₂=

2

x，P₂到平面AA₁B₁B的距离为x，
所以四面体P₁P₂AB₁的体积为V=

1

3

×

1

2

×(1-x)×1×x=

1

6

(x-x2)，
当x=

1

2

时，体积取得最大值：

1

24

．
故选A．

点评：本题考查正方形中，几何体的体积的求法，找出所求四面体的底面面积和高是解题的关键，考查计算能力．