题目内容
若函数y=f(x)满足f(a+x)+f(a-x)=2b(其中a,b不同时为0),则称函数y=f(x)为“准奇函数”,称点(a,b)为函数f(x)的“中心点”.现有如下命题:
①函数f(x)=sinx+1是准奇函数;
②函数f(x)=x3是准奇函数;
③若准奇函数y=f(x)在R上的“中心点”为(a,f(a)),则函数F(x)=f(x+a)-f(a)为R上的奇函数;
④已知函数f(x)=x3-3x2+6x-2是准奇函数,则它的“中心点”为(1,2);
其中正确的命题是 .(写出所有正确命题的序号)
①函数f(x)=sinx+1是准奇函数;
②函数f(x)=x3是准奇函数;
③若准奇函数y=f(x)在R上的“中心点”为(a,f(a)),则函数F(x)=f(x+a)-f(a)为R上的奇函数;
④已知函数f(x)=x3-3x2+6x-2是准奇函数,则它的“中心点”为(1,2);
其中正确的命题是
考点:抽象函数及其应用
专题:新定义,函数的性质及应用
分析:由诱导公式,计算f(-x)+f(x),即可判断①;由f(-x)+f(x)=0,则a=b=0,不满足条件,即可判断②;
运用准奇函数的定义和奇函数的定义,即可判断③;运用准奇函数的定义,化简整理,由恒等式知识求出中心,即可判断④.
运用准奇函数的定义和奇函数的定义,即可判断③;运用准奇函数的定义,化简整理,由恒等式知识求出中心,即可判断④.
解答:
解:对于①,函数f(x)=sinx+1有f(-x)+f(x)=sin(-x)+1+sinx+1=-sinx+sinx+2=2,
则y=f(x)为“准奇函数”,且(0,1)为f(x)的“中心点”,则①正确;
对于②,函数f(x)=x3,由f(-x)+f(x)=0,则a=b=0,不满足条件,则②不正确;
对于③,若准奇函数y=f(x)在R上的“中心点”为(a,f(a)),即有f(a+x)+f(a-x)=2f(a),
F(-x)+F(x)=f(a-x)-f(a)+f(x+a)-f(a)=2f(a)-2f(a)=0,则函数F(x)=f(x+a)-f(a)
为R上的奇函数,则③正确;
对于④,已知函数f(x)=x3-3x2+6x-2是准奇函数,则f(a+x)+f(a-x)
=(a+x)3-3(a+x)2+6(a+x)-2+(a-x)3-3(a-x)2+6(a-x)-2=(6a-6)x2+(2a3-6a2+12a-4)=2b,
即有6a-6=0且2a3-6a2+12a-4=2b,解得a=1,b=2,.则它的“中心点”为(1,2),则④正确.
故答案为:①③④.
则y=f(x)为“准奇函数”,且(0,1)为f(x)的“中心点”,则①正确;
对于②,函数f(x)=x3,由f(-x)+f(x)=0,则a=b=0,不满足条件,则②不正确;
对于③,若准奇函数y=f(x)在R上的“中心点”为(a,f(a)),即有f(a+x)+f(a-x)=2f(a),
F(-x)+F(x)=f(a-x)-f(a)+f(x+a)-f(a)=2f(a)-2f(a)=0,则函数F(x)=f(x+a)-f(a)
为R上的奇函数,则③正确;
对于④,已知函数f(x)=x3-3x2+6x-2是准奇函数,则f(a+x)+f(a-x)
=(a+x)3-3(a+x)2+6(a+x)-2+(a-x)3-3(a-x)2+6(a-x)-2=(6a-6)x2+(2a3-6a2+12a-4)=2b,
即有6a-6=0且2a3-6a2+12a-4=2b,解得a=1,b=2,.则它的“中心点”为(1,2),则④正确.
故答案为:①③④.
点评:本题考查新定义的理解和运用,考查函数的性质和运用,主要考查函数的对称性,运用定义和掌握定义是迅速解题的关键.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案
相关题目
已知函数f(x)=
,则方程f(x)=-1解的个数为( )
|
| A、0 | B、1 | C、2 | D、3 |
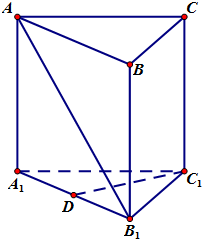 如图,直三棱柱ABC-A1B1C1中,AC=BC=
如图,直三棱柱ABC-A1B1C1中,AC=BC=| 2 |
| 3 |
(1)求证:C1D⊥AB1;
(2)若点F是BB1上的动点,求FB1的长度,使AB1⊥面C1DF.
设数列{an}满足an+an+1=3,且前三项之和S3=4,前四项之和S4=6,则a100=( )
| A、0 | B、1 | C、2 | D、3 |