题目内容
设数列{an}满足an+an+1=3,且前三项之和S3=4,前四项之和S4=6,则a100=( )
| A、0 | B、1 | C、2 | D、3 |
考点:数列递推式
专题:点列、递归数列与数学归纳法
分析:根据条件求出数列是周期数列即可得到结论.
解答:
解:当n=1时,足a1+a2=3,且前三项之和S3=4,
∴a3=4-3=1,
∵前四项之和S4=6,
∴a4=6-4=2,
∵an+an+1=3,∴an+1+an+2=3,
即an+an+1=an+1+an+2,
即an+2=an,
则数列{an}是周期为2的周期数列,
则a100=a4=2,
故选:C.
∴a3=4-3=1,
∵前四项之和S4=6,
∴a4=6-4=2,
∵an+an+1=3,∴an+1+an+2=3,
即an+an+1=an+1+an+2,
即an+2=an,
则数列{an}是周期为2的周期数列,
则a100=a4=2,
故选:C.
点评:本题主要考查数列项的求解,根据数列的递推关系求出数列是周期数列是解决本题的关键.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
 在某校的一次英语听力测试中用以下茎叶图记录了甲、乙两组各5名学生的听力成绩(单位:分)已知甲组数据的众数为15,乙组数据的中位数为17,则x、y的值分别为( )
在某校的一次英语听力测试中用以下茎叶图记录了甲、乙两组各5名学生的听力成绩(单位:分)已知甲组数据的众数为15,乙组数据的中位数为17,则x、y的值分别为( )| A、2,5 | B、5,5 |
| C、5,7 | D、8,7 |
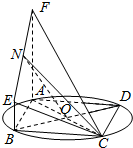 如图,已知AC,BD是圆O的两条互相垂直的直径,直角梯形ABEF所在平面与圆O所在平面互相垂直,其中∠FAB=∠EBA=90°,BE=2,AF=6,AC=4
如图,已知AC,BD是圆O的两条互相垂直的直径,直角梯形ABEF所在平面与圆O所在平面互相垂直,其中∠FAB=∠EBA=90°,BE=2,AF=6,AC=4