题目内容
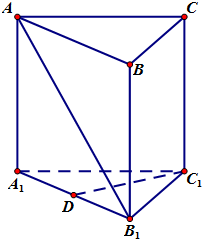 如图,直三棱柱ABC-A1B1C1中,AC=BC=
如图,直三棱柱ABC-A1B1C1中,AC=BC=| 2 |
| 3 |
(1)求证:C1D⊥AB1;
(2)若点F是BB1上的动点,求FB1的长度,使AB1⊥面C1DF.
考点:直线与平面垂直的判定,空间中直线与直线之间的位置关系
专题:空间位置关系与距离,空间向量及应用
分析:(1)以C1A1为X轴,C1B1为Y轴,C1C为Z轴建立空间直角坐标系,求得各点坐标,求得
,
的坐标,由
•
=0即可证明C1D⊥AB1;
(2)由(1)得AB1⊥C1D,只要AB1⊥DF时,就会有AB1⊥平面C1DF,求出
的坐标,由
•
=2-2
z=0,即可求得F点坐标,从而求得FB1的长度,使AB1⊥面C1DF.
| AB1 |
| C1D |
| AB1 |
| C1D |
(2)由(1)得AB1⊥C1D,只要AB1⊥DF时,就会有AB1⊥平面C1DF,求出
| DF |
| AB1 |
| DF |
| 3 |
解答:
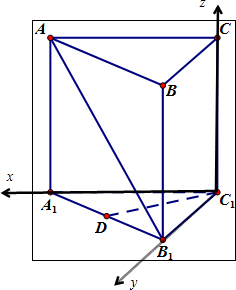 证明:(1)以C1A1为X轴,C1B1为Y轴,C1C为Z轴建立空间直角坐标系.
证明:(1)以C1A1为X轴,C1B1为Y轴,C1C为Z轴建立空间直角坐标系.
∴各点坐标为:C1(0,0,0)C(0,0,2
)B1(0,
,0)A1(
,0,0)D(
,
,0),
A(
,0,2
)B(0,
,2
)F(0,
,z),
∴
=(-
,
,-2
),
=(
,
,0),
∴
•
=0,
∴C1D⊥AB1;
(2)∵
=(-
,
,-2
),
∴AB1•C1D=0,
∴AB1⊥C1D,
∴只要AB1⊥DF时,就会有AB1⊥平面C1DF,
又∵
=(-
,
,z),
∴
•
=2-2
z=0,
∴当z=
时,AB1⊥DF,
即:F点坐标为(0,
,
)时,会使得AB1⊥平面C1DF,
∴可解得:|FB1|=
.
 证明:(1)以C1A1为X轴,C1B1为Y轴,C1C为Z轴建立空间直角坐标系.
证明:(1)以C1A1为X轴,C1B1为Y轴,C1C为Z轴建立空间直角坐标系.∴各点坐标为:C1(0,0,0)C(0,0,2
| 3 |
| 2 |
| 2 |
| ||
| 2 |
| ||
| 2 |
A(
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
∴
| AB1 |
| 2 |
| 2 |
| 3 |
| C1D |
| ||
| 2 |
| ||
| 2 |
∴
| AB1 |
| C1D |
∴C1D⊥AB1;
(2)∵
| AB1 |
| 2 |
| 2 |
| 3 |
∴AB1•C1D=0,
∴AB1⊥C1D,
∴只要AB1⊥DF时,就会有AB1⊥平面C1DF,
又∵
| DF |
| ||
| 2 |
| ||
| 2 |
∴
| AB1 |
| DF |
| 3 |
∴当z=
| ||
| 3 |
即:F点坐标为(0,
| 2 |
| ||
| 3 |
∴可解得:|FB1|=
| ||
| 3 |
点评:本题主要考查了直线与平面垂直的判定,空间中直线与直线之间的位置关系,考查了空间向量及其应用,考查了转化思想,属于中档题.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
已知S,A,B,C是球O表面上的点,SA⊥平面ABC,AB⊥BC,SA=AB=1,BC=
,则球O的内接正四面体的棱长等于( )
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、2
|
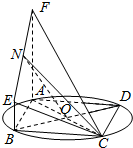 如图,已知AC,BD是圆O的两条互相垂直的直径,直角梯形ABEF所在平面与圆O所在平面互相垂直,其中∠FAB=∠EBA=90°,BE=2,AF=6,AC=4
如图,已知AC,BD是圆O的两条互相垂直的直径,直角梯形ABEF所在平面与圆O所在平面互相垂直,其中∠FAB=∠EBA=90°,BE=2,AF=6,AC=4