题目内容
已知函数f(x)=
(e为自然对数的底数),曲线y=f(x)在(1,f(1))处的切线与直线4x+3ey+1=0互相垂直.
(Ⅰ)求实数a的值;
(Ⅱ)若对任意x∈(
,+∞),(x+1)f(x)≥m(2x-1)恒成立,求实数m的取值范围;
(Ⅲ)设g(x)=
,Tn=1+2[g(
)+g(
)+g(
)+…+g(
)](n=2,3…).问:是否存在正常数M,对任意给定的正整数n(n≥2),都有
+
+
+…+
<M成立?若存在,求M的最小值;若不存在,请说明理由.
| (x+a)•ex |
| x+1 |
(Ⅰ)求实数a的值;
(Ⅱ)若对任意x∈(
| 2 |
| 3 |
(Ⅲ)设g(x)=
| (x+1)f(x) | ||
x(
|
| 1 |
| n |
| 2 |
| n |
| 3 |
| n |
| n-1 |
| n |
| 1 |
| T3 |
| 1 |
| T6 |
| 1 |
| T9 |
| 1 |
| T3n |
考点:导数在最大值、最小值问题中的应用,利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:(Ⅰ)求出导数,利用条件列出方程,即可求实数a的值;
(Ⅱ)转化条件为对x∈(
,+∞)恒成立,即m≤
对x∈(
,+∞)恒成立,构造函数t(x)=
(x>
),求出t(x)最小,即可得到实数m的取值范围.
(Ⅲ)通过g(x)=
,推出g(x)+g(1-x)=
=1,化简g(
)+g(
)=1,(k=1,2,3,…,n-1),推出Tn=n.然后求解
+
+
+…+
=
(
+
+
+…+
),取n=2m(m∈N*),利用放缩法推出
+
+
+…+
≥1+
,当m趋向于+∞时,1+
趋向于+∞.然后说明结果.
(Ⅱ)转化条件为对x∈(
| 2 |
| 3 |
| xex |
| 2x-1 |
| 2 |
| 3 |
| xex |
| 2x-1 |
| 2 |
| 3 |
(Ⅲ)通过g(x)=
| (x+1)f(x) | ||
x(
|
ex+
| ||
|
| k |
| n |
| n-k |
| n |
| 1 |
| T3 |
| 1 |
| T6 |
| 1 |
| T9 |
| 1 |
| T3n |
| 1 |
| 3 |
| 1 |
| 1 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| 1 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| m |
| 2 |
| m |
| 2 |
解答:
解:(Ⅰ)f′(x)=
=
依题意曲线y=f(x)在(1,f(1))处的切线与直线4x+3ey+1=0互相垂直.
得:f′(1)=
=
e,
∴a=0,
(Ⅱ)对任意的x∈(
,+∞),(x+1)f(x)≥m(2x-1)恒成立.
等价于xex-m(2x-1)≥0对x∈(
,+∞)恒成立,
即m≤
对x∈(
,+∞)恒成立
令t(x)=
(x>
),则m≤t(x)最小
∵t′(x)=
由t′(x)=0得:x=1或x=-
(舍去)
当x∈(
,1)时,t′(x)<0;
当x∈(1,+∞)时,t′(x)>0
∴t(x)在(
,1)上递减,在(1,+∞)上递增
∴t(x)最小=t(1)=e,
∴m≤e.
(Ⅲ)g(x)=
=
,
g(1-x)=
=
=
,
∴g(x)+g(1-x)=
=1,
因此有g(
)+g(
)=1,(k=1,2,3,…,n-1)
由Tn=1+2[g(
)+g(
)+g(
)+…+g(
)],
Tn=1+2[g(
)+g(
)+…+g(
)]
得2Tn=2+2[1+1+…+1]=2+2(n-1)=2n,∴Tn=n.
+
+
+…+
=
(
+
+
+…+
),取n=2m(m∈N*),
则
+
+
+…+
=
+
+(
+
)+(
+
+
+
)+…+
≥1+
×20+
×21+
×22+…+
×2m-1=1+
,
当m趋向于+∞时,1+
趋向于+∞.
所以,不存在正常数M,对任意给定的正整数n(n≥2),
都有
+
+
+…+
<M成立.
| [ex+(x+a)•ex](x+1)-(x+a)•ex |
| (x+1)2 |
| ex[x2+(a+1)x+1] |
| (x+1)2 |
依题意曲线y=f(x)在(1,f(1))处的切线与直线4x+3ey+1=0互相垂直.
得:f′(1)=
| (3+a)•e |
| 4 |
| 3 |
| 4 |
∴a=0,
(Ⅱ)对任意的x∈(
| 2 |
| 3 |
等价于xex-m(2x-1)≥0对x∈(
| 2 |
| 3 |
即m≤
| xex |
| 2x-1 |
| 2 |
| 3 |
令t(x)=
| xex |
| 2x-1 |
| 2 |
| 3 |
∵t′(x)=
| ex(2x2-x-1) |
| (2x-1)2 |
由t′(x)=0得:x=1或x=-
| 1 |
| 2 |
当x∈(
| 2 |
| 3 |
当x∈(1,+∞)时,t′(x)>0
∴t(x)在(
| 2 |
| 3 |
∴t(x)最小=t(1)=e,
∴m≤e.
(Ⅲ)g(x)=
| (x+1)f(x) | ||
x(
|
| ex | ||
|
g(1-x)=
| e1-x | ||
|
| e | ||
|
| ||
ex+
|
∴g(x)+g(1-x)=
ex+
| ||
|
因此有g(
| k |
| n |
| n-k |
| n |
由Tn=1+2[g(
| 1 |
| n |
| 2 |
| n |
| 3 |
| n |
| n-1 |
| n |
Tn=1+2[g(
| n-1 |
| n |
| n-2 |
| n |
| 1 |
| n |
得2Tn=2+2[1+1+…+1]=2+2(n-1)=2n,∴Tn=n.
| 1 |
| T3 |
| 1 |
| T6 |
| 1 |
| T9 |
| 1 |
| T3n |
| 1 |
| 3 |
| 1 |
| 1 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
则
| 1 |
| 1 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| 1 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| 6 |
| 1 |
| 7 |
| 1 |
| 8 |
| 1 |
| 2m |
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 23 |
| 1 |
| 2m |
| m |
| 2 |
当m趋向于+∞时,1+
| m |
| 2 |
所以,不存在正常数M,对任意给定的正整数n(n≥2),
都有
| 1 |
| T3 |
| 1 |
| T6 |
| 1 |
| T9 |
| 1 |
| T3n |
点评:本题考查函数的导数的综合应用,函数的最值的求法,构造法以及数列求和,放缩法的应用,难度大,考查知识面广.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
△ABC中,已知2A=B+C,且a2=bc,则△ABC的形状是( )
| A、两直角边不等的直角三角形 |
| B、顶角不等于90°,或60°的等腰三角形 |
| C、等边三角形 |
| D、等腰直角三角形 |
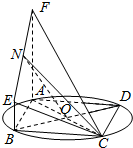 如图,已知AC,BD是圆O的两条互相垂直的直径,直角梯形ABEF所在平面与圆O所在平面互相垂直,其中∠FAB=∠EBA=90°,BE=2,AF=6,AC=4
如图,已知AC,BD是圆O的两条互相垂直的直径,直角梯形ABEF所在平面与圆O所在平面互相垂直,其中∠FAB=∠EBA=90°,BE=2,AF=6,AC=4