题目内容
已知等差数列{an}的前n项和为Sn,公差d≠0,S2=4,且a2,a5,a14成等比数列.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)从数列{an}中依次取出第2项,第4项,第8项,…,第2n项,…,按原来顺序组成一个新数列{bn},记该数列的前n项和为Tn,求Tn的表达式.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)从数列{an}中依次取出第2项,第4项,第8项,…,第2n项,…,按原来顺序组成一个新数列{bn},记该数列的前n项和为Tn,求Tn的表达式.
考点:数列的求和,等比数列的通项公式
专题:等差数列与等比数列
分析:(Ⅰ)由已知得:
,求出首项和公差,则等差数列{an}的通项公式可求;
(Ⅱ)把数列{an}的通项公式代入bn=a2n,然后利用分组求和及等比数列的通项公式得答案.
|
(Ⅱ)把数列{an}的通项公式代入bn=a2n,然后利用分组求和及等比数列的通项公式得答案.
解答:
解:(Ⅰ)依题意得:
,解得
.
∴an=a1+(n-1)d=1+2(n-1)=2n-1.
即an=2n-1;
(Ⅱ)由已知得,bn=a2n=2×2n-1=2n+1-1.
∴Tn=b1+b2+…+bn=(22-1)+(23-1)+…+(2n+1-1)
=(22+23+…+2n+1)-n=
-n=2n+2-4-n.
|
|
∴an=a1+(n-1)d=1+2(n-1)=2n-1.
即an=2n-1;
(Ⅱ)由已知得,bn=a2n=2×2n-1=2n+1-1.
∴Tn=b1+b2+…+bn=(22-1)+(23-1)+…+(2n+1-1)
=(22+23+…+2n+1)-n=
| 4(1-2n) |
| 1-2 |
点评:本题主要考查等比数列和等差数列的性质,考查了等比数列的前n项和的求法,考查了化归与转化思想方法,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若函数f(x)=2sin(2x+
)+a-1(a∈R)在区间[0,
]上有两个零点x1,x2(x1≠x2),则x1+x2-a的取值范围是( )
| π |
| 6 |
| π |
| 2 |
A、(
| ||||
B、[
| ||||
C、(
| ||||
D、[
|
已知S,A,B,C是球O表面上的点,SA⊥平面ABC,AB⊥BC,SA=AB=1,BC=
,则球O的内接正四面体的棱长等于( )
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、2
|
 在某校的一次英语听力测试中用以下茎叶图记录了甲、乙两组各5名学生的听力成绩(单位:分)已知甲组数据的众数为15,乙组数据的中位数为17,则x、y的值分别为( )
在某校的一次英语听力测试中用以下茎叶图记录了甲、乙两组各5名学生的听力成绩(单位:分)已知甲组数据的众数为15,乙组数据的中位数为17,则x、y的值分别为( )| A、2,5 | B、5,5 |
| C、5,7 | D、8,7 |
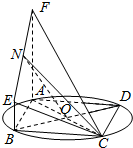 如图,已知AC,BD是圆O的两条互相垂直的直径,直角梯形ABEF所在平面与圆O所在平面互相垂直,其中∠FAB=∠EBA=90°,BE=2,AF=6,AC=4
如图,已知AC,BD是圆O的两条互相垂直的直径,直角梯形ABEF所在平面与圆O所在平面互相垂直,其中∠FAB=∠EBA=90°,BE=2,AF=6,AC=4