题目内容
18.在一球面上有A,B,C三点,如果AB=4$\sqrt{3}$,∠ACB=60°,球心O到平面ABC的距离为3,则球O的表面积为( )| A. | 36π | B. | 64π | C. | 100π | D. | 144π |
分析 设A、B、C三点所在圆的半径为r,圆心为O,从而可解得r=4,利用球心O到平面ABC的距离为3,可得答案.
解答 解:设A、B、C三点所在圆的半径为r,
∵AB=4$\sqrt{3},∠ACB={60°}$,
∴2r=$\frac{4\sqrt{3}}{sin60°}$=8,
∴r=4,
∵球心O到平面ABC的距离为3,
∴半径R=$\sqrt{9+16}$=5,
∴球O的表面积为4π•52=100π,
故选:C.
点评 本题考查了学生的空间想象力,考查学生的计算能力,求出A、B、C三点所在圆的半径是关键,属于中档题.

练习册系列答案
相关题目
9.设全集U={1,2,3,4,5,6},集合A={1,3,5},B={4,5,6},则(∁UA)∩B=( )
| A. | {2} | B. | {2,4} | C. | {4,6} | D. | {2,4,6} |
1.已知点A(0,2),抛物线C:y2=ax(a>0)的焦点为F,射线FA与抛物线C相交于点M,与其准线相交于点N,MK垂直准线于点K,若|KM|:|MN|=1:$\sqrt{5}$,则a的值等于( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 4 |
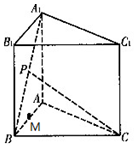 已知正三棱柱ABC-A1B1C的各条棱长都为a,P为A1B的中点,M为AB的中点,
已知正三棱柱ABC-A1B1C的各条棱长都为a,P为A1B的中点,M为AB的中点,