题目内容
9.设全集U={1,2,3,4,5,6},集合A={1,3,5},B={4,5,6},则(∁UA)∩B=( )| A. | {2} | B. | {2,4} | C. | {4,6} | D. | {2,4,6} |
分析 根据补集的定义知CUA={2,4,6},由此能求出(CuA)∩B.
解答 解:全集U={1,2,3,4,5,6},集合A={1,3,5},
∴∁UA={2,4,6},
∵B={4,5,6},
∴(∁UA)∩B={4,6}
故选:C.
点评 本题考查交、并、补集的混合运算,是基础题,解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
相关题目
20.在△ABC中,∠C=90°,且CA=CB=3,点M满足$\overrightarrow{BM}$=2$\overrightarrow{AM}$,则$\overrightarrow{CM}$$•\overrightarrow{CA}$=( )
| A. | 18 | B. | 3 | C. | 15 | D. | 9 |
17.已知函数f(x)=$\left\{\begin{array}{l}{(4-a)x-8,x≤6}\\{{a}^{x-5},x>6}\end{array}\right.$,若数列{an}满足an=f(n)(n∈N*),且{an}是递增数列,则实数a的取值范围是( )
| A. | [$\frac{16}{7}$,4) | B. | ($\frac{16}{7}$,4) | C. | (2,4) | D. | (1,4) |
1.设x>0,0<bx<ax<1,则正实数a,b的大小关系为( )
| A. | 1>a>b | B. | 1>b>a | C. | 1<a<b | D. | 1<b<a |
18.在一球面上有A,B,C三点,如果AB=4$\sqrt{3}$,∠ACB=60°,球心O到平面ABC的距离为3,则球O的表面积为( )
| A. | 36π | B. | 64π | C. | 100π | D. | 144π |
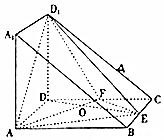 将棱长为2的正方体沿对角A1BAD1截去一半得到如图所示的几何体,点E,F分别是BC,DC的中点,AF与DE相交于O点.
将棱长为2的正方体沿对角A1BAD1截去一半得到如图所示的几何体,点E,F分别是BC,DC的中点,AF与DE相交于O点.