题目内容
13.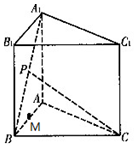 已知正三棱柱ABC-A1B1C的各条棱长都为a,P为A1B的中点,M为AB的中点,
已知正三棱柱ABC-A1B1C的各条棱长都为a,P为A1B的中点,M为AB的中点,(1)求证:AB⊥平面PMC;
(2)求点B到平面PAC的距离.
分析 (1)连接PM,CM,证明AB⊥PM,AB⊥CM,即可证明AB⊥平面PMC;
(2)利用等体积转化,求点B到平面PAC的距离.
解答 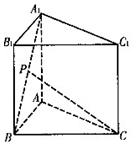 (1)证明:连接PM,CM (1分)
(1)证明:连接PM,CM (1分)
可知 PM∥AA1,而AB⊥AA1,∴AB⊥PM
又∵AB⊥CM,PM∩CM=M,∴AB⊥面PMC(6分)
(2)解:假设点B到平面PAC的距离:h,
四面体P-ABC的体积V=$\frac{1}{3}×\frac{1}{2}×a×\frac{{\sqrt{3}}}{2}a×\frac{1}{2}a=\frac{{\sqrt{3}}}{24}{a^3}$(8分)
∵△PAC中,AC=a,AP=$\frac{\sqrt{2}}{2}$a,PC=a,
∴${S_{△PAC}}=\frac{1}{2}×\frac{{\sqrt{2}}}{2}a×\sqrt{\frac{7}{8}}a=\frac{{\sqrt{7}}}{8}{a^2}$(9分)
∴${V_{P-ABC}}={V_{B-PAC}}⇒\frac{{\sqrt{3}}}{24}{a^3}=\frac{1}{3}×\frac{{\sqrt{7}}}{8}{a^2}×h⇒h=\frac{{\sqrt{21}}}{7}a$(12分)
点评 本题考查线面垂直的证明,考查点到平面的距离的求法,正确利用等体积转化是关键.

练习册系列答案
相关题目
1.设x>0,0<bx<ax<1,则正实数a,b的大小关系为( )
| A. | 1>a>b | B. | 1>b>a | C. | 1<a<b | D. | 1<b<a |
18.在一球面上有A,B,C三点,如果AB=4$\sqrt{3}$,∠ACB=60°,球心O到平面ABC的距离为3,则球O的表面积为( )
| A. | 36π | B. | 64π | C. | 100π | D. | 144π |
5.如图是一个棱锥的三视图,则该棱锥的体积为( )


| A. | 12 | B. | 4 | C. | 6 | D. | 2 |
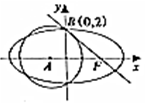 如图,点F为椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)右焦点,圆A:(x-t)2+y2=$\frac{16}{3}$(t<0)与椭圆C的一个公共点为B(0,2),且直线FB与圆A相切于点B.
如图,点F为椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)右焦点,圆A:(x-t)2+y2=$\frac{16}{3}$(t<0)与椭圆C的一个公共点为B(0,2),且直线FB与圆A相切于点B.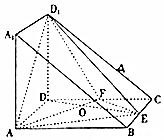 将棱长为2的正方体沿对角A1BAD1截去一半得到如图所示的几何体,点E,F分别是BC,DC的中点,AF与DE相交于O点.
将棱长为2的正方体沿对角A1BAD1截去一半得到如图所示的几何体,点E,F分别是BC,DC的中点,AF与DE相交于O点.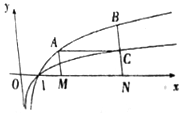 如图,过函数f(x)=logcx(c>1)的图象上的两点A,B作x轴的垂线,垂足分别为M(a,0),N(b,0)(b>a>1),线段BN与函数g(x)=logmx(m>c>1)的图象交于点C,且AC与x轴平行.
如图,过函数f(x)=logcx(c>1)的图象上的两点A,B作x轴的垂线,垂足分别为M(a,0),N(b,0)(b>a>1),线段BN与函数g(x)=logmx(m>c>1)的图象交于点C,且AC与x轴平行.